- 双曲线及其性质
- 共531题
已知点P是双曲线C:
正确答案
解析
解:在三角形F1F2P中,点N恰好平分线段PF2,点O恰好平分线段F1F2,
∴ON∥PF1,又ON的斜率为
∴tan∠PF1F2=
在三角形F1F2P中,设PF2=bt,PF1=at,
根据双曲线的定义可知|PF2|﹣|PF1|=2a,∴bt﹣at=2a,①
在直角三角形F1F2P中,|PF2|2+|PF1|2=4c2,∴b2t2+a2t2=4c2,②
由①②消去t,得
又c2=a2+b2,
∴a2=(b﹣a)2,即b=2a,
∴双曲线的离心率是

故选A。
知识点
设斜率为






(1)若点M为弦AB的中点,求
(2)把题设中的椭圆一般化为
(i)根据(1)的运算结果,写出一个关于
(ii)根据以上探究,在双曲线
正确答案
见解析。
解析
(1)设
且有

(2)(i)斜率为






逆命题:斜率为







证明如下:设直线


得



将



即点M为弦AB的中点。
(ii)斜率为






知识点
已知点F1、F2是双曲线


正确答案
解析
∵

∴

知识点
已知F1、F2是双曲线
正确答案
解析
设



|PF1| =c
故
知识点
5.双曲线
正确答案
解析
双曲线


知识点
7.设






正确答案
解析
略
知识点
已知点








(1)求曲线
(2)设







正确答案
见解析
解析
(1)设







(2)①当直线

则


②当直线


联立方程




又
即
将






令


当且仅当

知识点
已知A、B为抛物线C:y2 = 4x上的两个动点,点A在第一象限,点B在第四象限l1、l2分别过点A、B且与抛物线C相切,P为l1、l2的交点.
(1)若直线AB过抛物线C的焦点F,求证:动点P在一条定直线上,并求此直线方程;
(2)设C、D为直线l1、l2与直线x = 4的交点,求
正确答案
见解析。
解析
(1)设


易知



由

由直线


于是,


同理,

联立



∵ 





∴ 

∴ 


或解:设





∴ 点


∴ 直线

由直线


∴ 


(2)由(1)知,



∴ 
∴ 
设


由


∴ 
设

∴ 





在区间
∴ 


∴ 当

即



知识点
设点P是双曲线
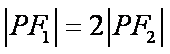
正确答案
解析
由已知得,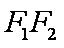
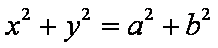
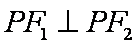

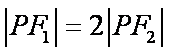
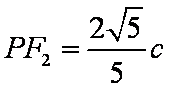
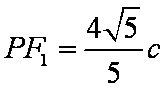
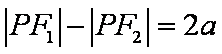
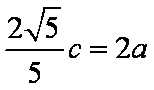
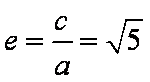
知识点
11.已知双曲线
正确答案
解析
由题意,c=
∴a2+b2=c2=25. ①
又双曲线的渐近线为y=±


则由①②解得a=3,b=4,∴双曲线方程为
知识点
扫码查看完整答案与解析








































