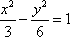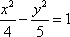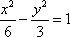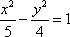- 双曲线及其性质
- 共531题
双曲线
正确答案
解析
略
知识点
已知函数
(1)若


(2)求
(3)若函数



正确答案
见解析。
解析
(1)


又




即
(2)




当


当





(3)(i)当

由(2)知


当


又当

当



所以,


等价于



(ii)当






原问题等价于


综上,

知识点
已知双曲线

正确答案
解析
设双曲线C :



又



又




知识点
已知双曲线







正确答案
解析
略
知识点
如图,已知椭圆








(1)求椭圆和双曲线的标准方程;
(2)设直线




(3)是否存在常数


正确答案
见解析。
解析
(1)设椭圆的半焦距为


所以 

又

故椭圆的标准方程为
由题意设等轴双曲线的方程
因此 双曲线的标准方程为
(2)设
则 
因为 点


因此 
即 
(3)由于


由根与系数的关系得
所以

同理可得
则 
又 
所以 
故
因此 存在

知识点
直线


正确答案
解析
略
知识点
已知双曲线

且双曲线


正确答案
解析
略
知识点
已知曲线
(1)若曲线C在点



(2)对任意实数




正确答案
(1) 
(2)b的取值范围是
解析
(1)
因为曲线C在点(0,1)处的切线为L:
所以

解得

(2)法1:
对于任意实数a,曲线C总在直线的






令
①若a=0,则
所以实数b的取值范围是
②若

由


------------------------------------11分
所以

所以实数b的取值范围是
综上,实数b的取值范围是
法2:对于任意实数a,曲线C总在直线的






令


令

由


------------------------------------11分
所以 

实数b的取值范围是
知识点
已知双曲线E的中心在原点,F(3,0)是E的焦点,过F的直线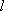
正确答案
解析
设双曲线E的方程为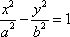
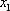
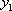
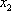
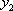
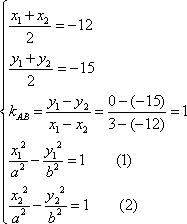
(1)-(2)得 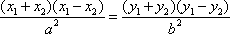
所以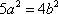
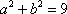
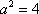
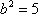
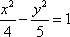
知识点
已知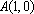
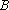
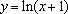
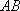
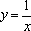
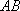
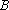
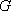
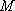
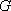
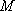

正确答案
解析
略
知识点
扫码查看完整答案与解析