- 双曲线及其性质
- 共531题
已知点


(1)求动点P的轨迹C的方程;
(2)直线
正确答案
(1)动点P的轨迹C的方程为
(2)
解析
(1)依题意,动点P的轨迹C是以

设轨迹C的方程为
所以动点P的轨迹C的方程为 
(2)解法一:因为

联立方程组
消元得:


由抛物线定义知:

又由



则

所以
因为FABD为平行四边形,所以
所以

解得


解法二:因为

联立方程组


故点

当



根据韦达定理有

又因为四边形是平行四边形,所以
将坐标代入有
代入①有

整理得
此时(*)的判别式
当

知识点
正确答案
见解析
解析
(1)原曲线方程可化简得:
由题意可得:
(2)由已知直线代入椭圆方程化简得:

由韦达定理得:

设






欲证


即
将①②代入易知等式成立,则
知识点
已知点F,B分别为双曲线C:
正确答案
解析
略
知识点
双曲线


正确答案
解析
略
知识点
设曲线C的方程为(x-2)2+(y+1)2=9,直线l的方程x-3y+2=0,则曲线上的点到直线l的距离为
正确答案
解析
略
知识点
已知双曲线 




正确答案
解析
略
知识点
设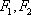
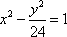
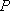
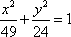
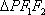
正确答案
24
解析
略
知识点
已知双曲线

正确答案
解析
略
知识点
已知双曲线C的焦点、实轴端点恰好是椭圆
正确答案
解析
略
知识点
已知椭圆C的一个焦点在抛物线 


(1)求椭圆C的方程;
(2)设过点M(2,0)的直线与椭圆C相交于两点A、B,满足 

正确答案
见解析
解析
知识点
扫码查看完整答案与解析




























