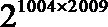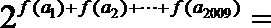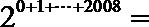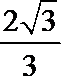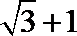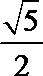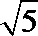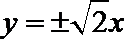- 双曲线及其性质
- 共531题
13.双曲线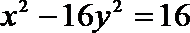
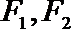
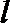
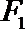
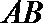
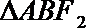
正确答案
40
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数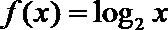
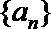


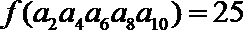
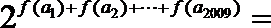
正确答案
解析
因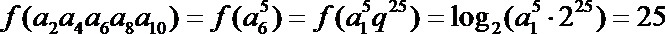
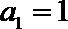
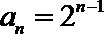
所以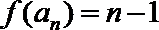
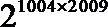
知识点
11.设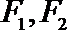


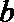

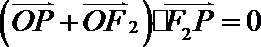
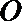

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 若双曲线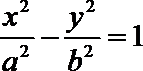
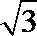
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知二次曲线Ck的方程:
(1)分别求出方程表示椭圆和双曲线的条件;
(2)若双曲线Ck与直线
(3)设









正确答案
(1)当且仅当
即
当且仅当
即
(2)解法一:
∵双曲线实轴最长,∴

此时双曲线方程为
解法二:若

不妨设双曲线方程为
联立
得
∴实轴最长的方程为
解法三:不妨先求得


设直线与双曲线左支交点为
∴实轴最长的方程为
解法四:设双曲线与直线公共点为
则
即

∴实轴最长的方程为
(3)由(1)知

结合图像的几何间无公共点,任意两双曲线之间也无公共点,
设
则根据椭圆、双曲线定义及


所以
所以这样的
且
解析
解析已在路上飞奔,马上就到!
知识点
7.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知抛物线










正确答案
解析
当直线

知识点
21.如图,四棱锥






(1)求证:
(2)求

(3)求点

正确答案
∵

∴以


∵
∴ 
(1)∴

(2) ∵
设面
∴
∵

即

(3)∵
设面
设
∴点

解析
解析已在路上飞奔,马上就到!
知识点
11. 若双曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析