双曲线及其性质
共531题

双曲线及其性质
共531题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 4 分

5．双曲线上任意一点到两条渐近线的距离的乘积为____．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

7．函数在同一平面直角坐标系内的大致图象为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化对数函数的图像与性质知图选式与知式选图双曲线的定义及标准方程

题型：填空题

填空题 · 4 分

8．已知双曲线（m＞0）的一条渐近线方程为y=x，它的一个焦点恰好在抛物线y2=ax的准线上，则 a=________．

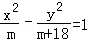
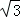
正确答案

±24

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：简答题

简答题 · 12 分

20．已知双曲线与圆相切，过的一个焦点且斜率为的直线也与圆相切．

（Ⅰ）求双曲线的方程；

（Ⅱ）是圆上在第一象限的点，过且与圆相切的直线与的右支交于、两点，的面积为，求直线的方程．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：简答题

简答题 · 16 分

22．设，为坐标平面上的点．直线与抛物线交于点（异于点）．

（1）对任意，点在抛物线上，试问当为何值时，点在某一圆上?并求出该圆的方程；

（2）若点在椭圆上运动，试问能否保持在一双曲线上?若能，求出该双曲线的方程．若不能，说明理由；

（3）对（1）中点所在的圆，设为圆上两点，且满足，试寻找一个定圆，使得恒与圆相切．

正确答案

（1）直线，与抛物线联立得，依题意，

，当时，在圆上；

（2）若点在椭圆上运动，则，

（方法1）两边同除以得，，

∴点在双曲线上；

（方法2）设，则代入上式，

得，

即，∴点在双曲线上；

（3）（方法1）设，则，

由得

① 当直线的斜率为零时，

设的方程为，于是（舍负）

②当直线的斜率不为零时，

设的方程为，代入圆的方程得

，于是，

即原点到直线的距离，与无关，

∴直线总与圆相切．

（方法2）设，原点到直线的距离为

则，

即

注意到圆是的外接圆，

∴，∴

即原点到直线的距离为定值，

∴直线总与圆相切．

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程双曲线的定义及标准方程圆锥曲线的定点、定值问题圆锥曲线中的探索性问题直线、圆及圆锥曲线的交汇问题

题型：填空题

填空题 · 4 分

11．已知⊙O的方程是x2+y2﹣2=0，⊙O'的方程是x2+y2﹣8x+10=0，由动点P向⊙O和⊙O'所引的切线长相等，则动点P的轨迹方程是________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

13．已知曲线，曲线（t为参数），则与的位置关系为____________．

正确答案

相离

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

16．曲线为参数）与曲线的交点个数为__________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：填空题

填空题 · 5 分

15．已知是双曲线：的左焦点，是双曲线的虚轴，是的中点，过的直线交双曲线于，且，则双曲线离心率是____________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：单选题

单选题 · 5 分

8．已知F1、F2为双曲线C：的左、右焦点，点P在C上，|PF1|=|2PF2|，则cos∠F1PF2=( )

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

继续学习学习下一知识点

下一知识点 : 抛物线及其性质

百度题库 > 高考 > 理科数学 > 双曲线及其性质

扫码查看完整答案与解析