- 双曲线及其性质
- 共531题
21.已知















(1)求轨迹
(2)设点



正确答案
解:
(1)由|PF1|-|PF2|=2<|F1F2|知,点P的轨迹S是以F1、F2为焦点的双曲线右支.
由c=2,2a=2,∴b2=3.故轨迹S的方程为x2-=1 (x≥1)
(2)当直线l的斜率存在时,设直线方程为y=k(x-2),P(x1,y1),Q(x2,y2)
与双曲线方程联立消y得(k2-3)x2-4k2x+4k2+3=0.
∴


=[4x1x2-2(x1+x2)+1]=x1x2-+
=-+=+=+>.
当斜率不存在时,|AP|·|BQ|=,∴λ的最小值为.
此时,|PQ|=6,|MF2|=3,S△PMQ=|MQ|·|PQ|=9.
解析
解析已在路上飞奔,马上就到!
知识点
6.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知双曲线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知中心在原点的双曲线C的右焦点为(2,0),右顶点为(
(I)求双曲线C的方程;
(II)若直线
正确答案
解:
(I)设双曲线方程为
由已知得
故双曲线C的方程为
(II)联立

可得
整理得3k2=4m+1
将②代入①,得m2-4m>0,∴m<0或m>4
又3k2=4m+1>0(k≠0),即m>-
∴m的取值范围是(-
解析
解析已在路上飞奔,马上就到!
知识点
6.与双曲线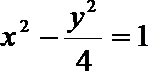
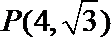
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若双曲线
正确答案
2
解析
知识点
2.已知双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在平面直角坐标系xOy中,已知y=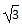
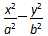
正确答案
2
解析
由题意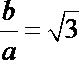
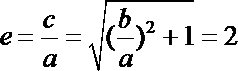
知识点
11.已知双曲线中心在原点且一个焦点为




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析