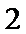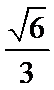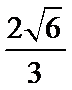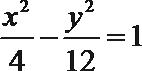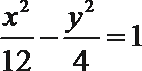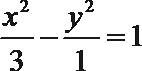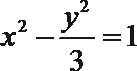- 双曲线及其性质
- 共531题
14.已知双曲线






正确答案
解析
甴已知可得A(-a,0),F(c,0),所以





考查方向
解题思路
先确定点A,F的坐标,然后求得向量


易错点
本题必须注意
知识点
11.P是双曲线



正确答案
解析
由题知


∴

∴



考查方向
本题主要考查利用双曲线的定义及几何性质研究离心率的思想方法,也在题目的解决中考查了正弦定理的应用,意在考查考生的数形结合思想和考生的运算求解能力,在近几年的各省高考题出现的频率较高,常独立命题,或是与三角函数等知识点交汇命题,较难。
解题思路
1、先根据题意做图,从而发现得到离心率时要找到

2、在

易错点
1、本题易在构造几何模型上出错。
2、本题易在解决问题时未能把双曲线定义与三解形性质相结合而出错。
知识点
10.抛物线

正确答案
解析
由题意可知,得到抛物线准线与双曲线的三个交点的坐标分别为:A(-2,0),B(2,

考查方向
解题思路
根据题意作出图形,求解面积
易错点
交点坐标求错。
知识点
9.已知双曲线



正确答案
解析
由



考查方向
解题思路
根据所给条件判断逻辑关系
易错点
充分条件和必要条件理解错误,双曲线相关性质运用不恰当
知识点
10. 在平面直角坐标系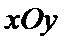
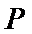
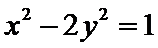
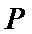
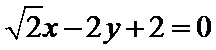
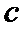
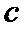
正确答案
解析
双曲线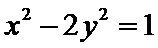

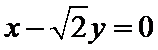

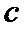
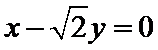
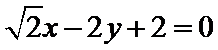
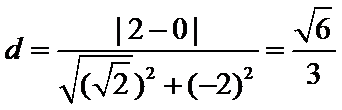
A选项不正确,B选项不正确,D选项不正确,所有选C选项.
考查方向
解题思路
求已知双曲线的渐近线方程,其到已经直线的距离即为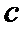
易错点
1、本题易将已经双曲线的渐近线方程代错. 2、本题不容易理解c的最大值是什么,从而使题解无法进行.
知识点
11. 已知双曲线




正确答案
解析
解:双曲线

以F1F2为直径的圆的方程为x2+y2=c2,
将直线

即有M(a,b),又A(-a,0),
由于∠MAB=30°,则直线AM的斜率为
又
则3b2=4a2=3(c2-a2),
即有3c2=7a2,
则离心率
故选B.
考查方向
双曲线的简单性质.
解题思路
求出双曲线的渐近线方程和圆的方程,求出交点M,再由两点的斜率公式,得到a,b的关系,再由离心率公式即可得到所求值.
易错点
建立a,b,c之间的关系,容易出错.
教师点评
本题考查双曲线的方程和性质,考查直线和圆的位置关系,直线的斜率公式,考查离心率的求法,属于基础题.
知识点
7.设双曲线

同,则此双曲线的方程为
正确答案
解析
由c=1,且焦点在y轴上,得a=2b。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
本题主要考查双曲线的标准方程
解题思路
1、求出c;
2、利用a,b,c关系求a,b,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在判断焦点位置时发生错误。
知识点
1.若双曲线
正确答案
解析
试题分析:本题属于双曲线中的基本问题,题目的难度是简单。
考查方向
本题主要考查了双曲线的标准方程,在近几年的各省高考题出现的频率较高。
解题思路
本题考查双曲线的焦点位置,解题步骤如下:
(1)由题可知,易得x2的系数为正,y2系数为负。
(2)令2-k>0,k-1<0,解得k<1.
易错点
本题易在求解时把分母平方运算。
知识点
11.双曲线C:



正确答案
解析
因为双曲线C:







考查方向
解题思路
因为双曲线C:







易错点
本题易在判定点

知识点
7.已知双曲线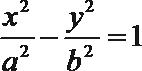
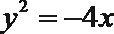
正确答案
解析
双曲线的左焦点为(-2,0),即c=2,所以a=1,b2=3,所以选D
考查方向
本题主要考查双曲线与抛物线的几何性质,属于简单题
解题思路
先求出a,b的值,进而求解问题
易错点
双曲线的标准方程等基础概念
知识点
扫码查看完整答案与解析