- 双曲线及其性质
- 共531题
已知双曲线
正确答案
知识点
已知F1,F2是双曲线E: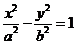
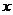
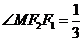
正确答案
知识点
13.双曲线
正确答案
2
知识点
5.已知方程
正确答案
知识点
5.已知方程
正确答案
知识点
13.已知双曲线E1:
正确答案
2
知识点
6.已知双曲线
正确答案
知识点
13.已知双曲线E1:
正确答案
2
知识点
设椭圆E的方程为



25.求E的离心率e;
26.设点C的坐标为(0,-b),N为线段AC的中点,证明:MN
正确答案
(Ⅰ)
解析
(Ⅰ)解:由题设条件知,点


进而

证:由




又
由(Ⅰ)得计算结果可知


考查方向
解题思路
由题设条件,可得点





易错点
计算能力弱,圆锥曲线相关知识掌握不牢固,不系统
正确答案
详见解析.
解析
(Ⅱ)证:由




又
由(Ⅰ)得计算结果可知


考查方向
解题思路
利用向量的坐标表示求解,得到坐标数量积为0,进而得到线段垂直。
易错点
圆锥曲线的相关性质、概念、公式记忆错误,计算能力弱
13.双曲线



正确答案
2
解析
考查方向
解题思路
在双曲线的几何性质中,渐近线是其独特的一种性质,渐近线方程与双曲线方程的待定系数之间的关系是考查的重点内容,双曲线方程的方法以及双曲线定义和双曲线标准方程的应用都和与椭圆有关的问题相类似.因此,双曲线与椭圆的标准方程可统一为





易错点
双曲线渐近线方程与双曲线方程待定系数之间的关系
知识点
扫码查看完整答案与解析














