双曲线及其性质_章节学习

1

题型：简答题

|

简答题 · 12 分

设，是曲线在点处的切线与x轴交点的横坐标.

19.求数列的通项公式；

20.记，证明.

第(1)小题正确答案及相关解析

正确答案

（1）

解析

（Ⅰ）解：，曲线在点处的切线斜率为.

从而切线方程为.令，解得切线与轴交点的横坐标.

考查方向

1.曲线的切线方程；2.数列的通项公式；3.放缩法证明不等式.

解题思路

（Ⅰ）对题中所给曲线的解析式进行求导，得出曲线在点处的切线斜率为.从而可以写出切线方程为.令.解得切线与轴交点的横坐标.

易错点

求导错误，不会联系导数和曲线之间的关系。

第(2)小题正确答案及相关解析

正确答案

（2）.

解析

（Ⅱ）证：由题设和（Ⅰ）中的计算结果知

.

当时，.

当时，因为，

所以.

综上可得对任意的，均有.

考查方向

1.曲线的切线方程；2.数列的通项公式；3.放缩法证明不等式.

解题思路

（Ⅱ）要证，需考虑通项，通过适当放缩能够使得每项相消即可证明.思路如下：先表示出，求出初始条件当时，.当时，单独考虑，并放缩得，所以

，综上可得对任意的，均有.

易错点

证明不等式成立时，找不到合理适当的放缩不等式

1

题型：单选题

|

单选题 · 5 分

7．已知双曲线：的离心率，且其右焦点，则双曲线的方程为

A

B

C

D

正确答案

B

解析

因为所求双曲线的右焦点为且离心率为，所以，，所以所求双曲线方程为，故选．

考查方向

本题考查双曲线的标准方程及其简单基本性质，属于基础题。

解题思路

根据离心率方程，双曲线自身性质方程，及焦点值求出a、b的值。

易错点

椭圆，双曲线的离心率公式要分清楚。

知识点

双曲线的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

6.若双曲线的一条渐近线经过点（3，-4），则双曲线的离心率为

A

B

C

D

正确答案

D

解析

由题意得，所以，所以，故选D选项。

考查方向

本题主要考察双曲线的性质，意在考察考生的运算求解能力。

解题思路

直接根据题意得到a,b,c之间的关系即可得到答案。

易错点

弄错渐近线方程导致结果出错。

知识点

双曲线的定义及标准方程双曲线的几何性质

1

题型：填空题

|

填空题 · 5 分

10．已知双曲线的一条渐近线过点，且双曲线的一个焦点在抛物线的准线上，则双曲线的方程为___________

正确答案

解析

将代入渐近线方程，得a=2b. c=,c2=a2+b2, a2+.

考查方向

本题主要考查了双曲线的方程及双曲线与抛物线的基本知识。

解题思路

本题考查运用双曲线的渐近线方程及抛物线的准线方程，求a,b，解题步骤如下：将代入渐近线方程，得a=2b. 由双曲线的一个焦点在抛物线的准线上，可知c=,c2=a2+b2, a2+.

易错点

本题必须注意审题，忽视则会出现错误。

知识点

双曲线的定义及标准方程双曲线的几何性质抛物线的标准方程和几何性质

1

题型：填空题

|

填空题 · 5 分

14.双曲线的左，右焦点分别为，记，以坐标原点为圆心，为半径的圆与双曲线在第一象限的交点为，若，则点的横坐标为．

正确答案

解析

设P点的横坐标为,

，

所以。

考查方向

本题考查了双曲线的性质和圆的几何性质。属于常考题。

解题思路

利用圆与双曲线的性质，以及双曲线的定义可得C的值，利用焦半径公式可得结论。

易错点

P到两个焦点的距离问题。

知识点

双曲线的定义及标准方程

1

题型：单选题

|

单选题 · 4 分

2．“孩提知爱长知钦，古圣相传只此心。大抵有基方筑室，未闻无址忽成岑。留情传扫翻蓁塞，着意精微转陆沉。珍重友朋相切琢，须知至乐在于今”。该诗反映了（）

A圣人之道存于经典，孔孟之要在于天理

B发明本心，尊我德性，确立自我主体是根本

C倡导重义轻利的价值观，主张以义制利

D格物致知，读书穷理，循章摘句，博览群书

正确答案

B

解析

此题考查学生对材料的理解能力。材料的大意是：人有天赋道德之心，自古圣贤相传的也只是这种本心。将精力花费到注解诠释古代经典上，以探求精微大义，只会使人迷惘。这属于陆王心学的观点，故选Ｂ。A项、D项是程朱理学观点，B项是陆王心学方法论思想，C项是孟子思想，故正确答案选择B项。

考查方向

中国传统文化主流思想的演变-宋明理学-陆王心学

解题思路

此题考查学生对材料的理解能力。材料的大意是：人有天赋道德之心，自古圣贤相传的也只是这种本心。将精力花费到注解诠释古代经典上，以探求精微大义，只会使人迷惘。这属于陆王心学的观点，故选Ｂ。A项、D项是程朱理学观点，B项是陆王心学方法论思想，C项是孟子思想，故正确答案选择B项。

易错点

此题易错点在于：1.对材料主旨意思理解不准而误选；2.对选项信息不能有效形成知识迁移而出现知识漏洞。

知识点

双曲线的定义及标准方程

1

题型：填空题

|

填空题 · 5 分

16．在双曲线（a＞0，b＞0）中，A1，A2是左、右顶点，F是右焦点，B是虚轴的上端点，若在线段BF上存在点P，使得△PA1A2构成以A1A2为斜边的直角三角形，则双曲线离心率e的取值范围是_____________．

正确答案

解析

由题意，F（c，0），B（0，b），则直线BF的方程为bx+cy-bc=0，若在线段BF上存在点P，使得△PA1A2构成以A1A2为斜边的直角三角形，则即，由于e>1,解得

考查方向

本题主要考查了双曲线的几何性质，考查考生分析问题和解决问题的能力。

解题思路

根据题意写出线段BF所在直线方程，借助△PA1A2构成以A1A2为斜边的直角三角形构建原点到直线的距离小于或等于a,从而解出e的取值范围。

易错点

△PA1A2构成以A1A2为斜边的直角三角形的转化

知识点

双曲线的定义及标准方程双曲线的几何性质

1

题型：单选题

|

单选题 · 5 分

11.已知A，B为双曲线E的左，右顶点，点M在E上，∆ABM为等腰三角形，且顶角120°，则E的离心率为( )

A

B2

C

D

正确答案

D

知识点

双曲线的定义及标准方程双曲线的几何性质

1

题型：单选题

|

单选题 · 5 分

9．已知直线l与双曲线C:x2-y2=2的两条渐近线分别交于A，B两点，若AB的中点在该双曲线上，O为坐标原点，则△A OB的面积为（）

A

B1

C2

D4

正确答案

C

解析

根据题意，可知，想要AB的中点在该双曲线上，由于是选择题，则直线可以是垂直于x轴的直线，所以可知，三角形的面积为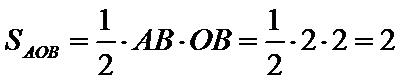，所以选C

考查方向

双曲线的图象的性质与特征,双曲线的渐近线

解题思路

根据条件找到三角形AOB的位置，进而求面积

易错点

对相关概念理解不透彻

知识点

双曲线的定义及标准方程

1

题型：单选题

|

单选题 · 5 分

8.过双曲线（）的左顶点作斜率为的直线，若直线与双曲线的两条渐近线分别相交于点，，且，则双曲线的离心率为（）

A

B

C

D

正确答案

B

解析

由题意可知P(-1,0),所以直线L的方程为y=x+1，两条渐近线的方程为y=-bx或y=bx,所以可得Q点横坐标为，R点的横坐标为，因为

所以，所以，所以b=3,

C=,所以，所以选B

考查方向

双曲线的标准方程；双曲线的性质及其图象的特征

解题思路

先求出R和Q的横坐标，然后求出b的值，进而求出c,然后根据离心率公式答案可得

易错点

计算能力弱，离心率公式记混淆

知识点

向量在几何中的应用双曲线的定义及标准方程双曲线的几何性质直线、圆及圆锥曲线的交汇问题

热门试卷

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点

正确答案

解析

考查方向

解题思路

易错点

知识点