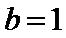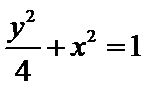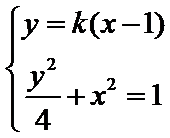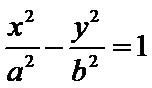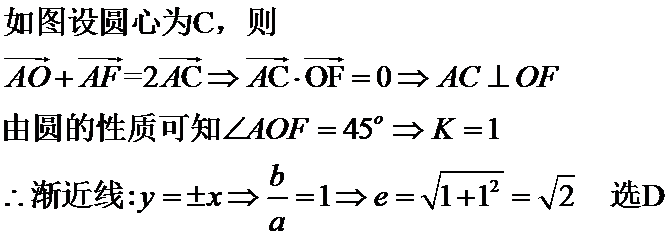- 双曲线及其性质
- 共531题
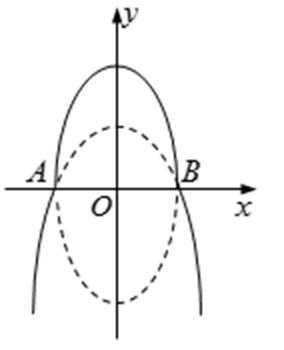
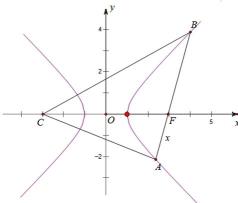
如图,曲线
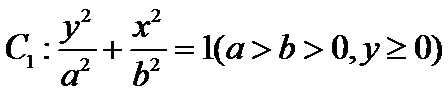
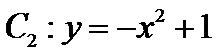
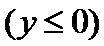
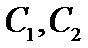
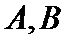
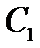
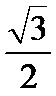
23.求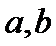
24.过点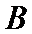

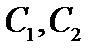
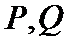
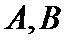
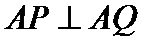

正确答案
(1)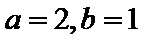
解析
(Ⅰ)因为抛物线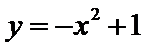
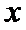
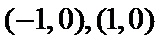
由因为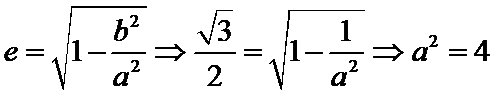
考查方向
解题思路
先根据抛物线与x轴的交点求出b的值,后利用离心率求出a的值;
易错点
不知道抛物线与x轴的交点即为b的值;
正确答案
(2)
解析
(Ⅱ)因为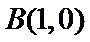
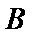
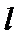
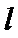
设直线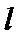
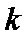
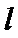
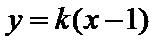
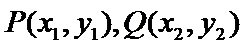
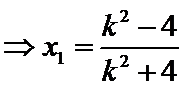
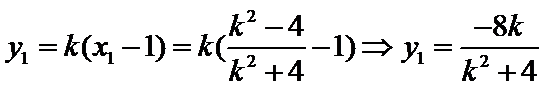
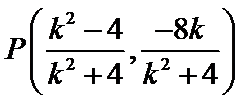
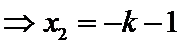
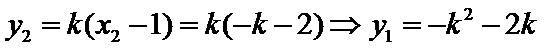
由
化简得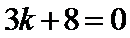
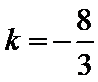
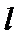
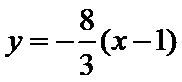
考查方向
解题思路
设出直线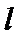
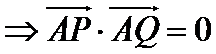
易错点
不会转化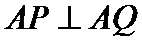
9. 等腰直角三角形ABC中,A=90°,A,B在双曲线E的同一支上,且线段AB通过双曲线的一个焦点,C为双曲线E的另一个焦点,则该双曲线的离心率为
正确答案
解析
设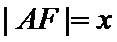
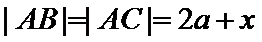
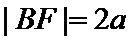
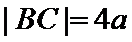
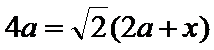
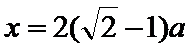
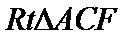
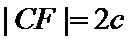
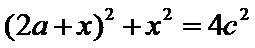
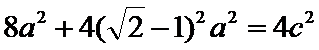

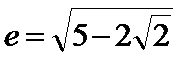
考查方向
解题思路
1)利用等腰三角形和双曲线的定义得到相关边的长度;
2)利用勾股定理和离心率公式进行求解.
易错点
本题易在选择双曲线的定义出现错误,易忽视双曲线的定义的灵活运用.
知识点
6.经过点(2,1),且渐近线与圆
正确答案
解析
设渐近线方程为
∴渐近线为
∴设双曲线方程为
考查方向
解题思路
1)设渐近线方程
2)利用渐近线写出含参双曲线方程,带入坐标直接得出结果
易错点
本题易在双曲线焦点的判断
知识点
15.已知



正确答案
2
解析
由题意得








考查方向
解题思路
1.先根据题意先表示出


易错点
1.点(m,n)的坐标求错;2.不会建立关于a,b,c之间的关系。
知识点
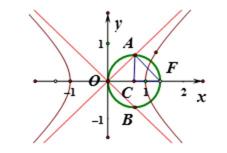
6.已知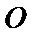

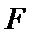
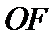
圆交双曲线的渐近线于两点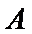
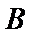
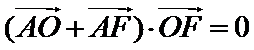
心率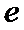
正确答案
解析
由题意作图
考查方向
解题思路
1、根据题意画出简图
2、找到向量的性质直接得出a,b的关系
易错点
主要易错于圆的性质的判断,以及向量的几何意义的判断
知识点
14.椭圆






正确答案
解析
不妨设双曲线










考查方向
解题思路
1.先求出双曲线的渐近线方程;2.根据





易错点
1.对于题中给出的条件
知识点
6.过双曲线



正确答案
解析
设




考查方向
解题思路
1.根据直线间的垂直关系求出

易错点
1.不会转化过双曲线

知识点
9.已知双曲线







正确答案
解析
因为


由平面几何知识得





考查方向
解题思路


易错点
不会画等腰三角形
知识点
10.设双曲线

正确答案
解析
由题意






所以
所以
因此渐近线的斜率取值范围是
考查方向
解题思路
求双曲线的渐近线的斜率取舍范围的基本思想是建立关于


易错点
解题中要注意椭圆与双曲线中
知识点
10.双曲线








正确答案
解析
由题意知:






考查方向
解题思路
1.先根据题意求出M点到坐标;2.根据直线



易错点
1.不会求M点的坐标;
2.不会转化题中的倾斜角为45度。
知识点
扫码查看完整答案与解析