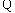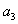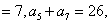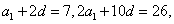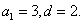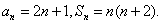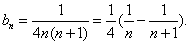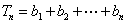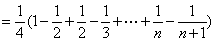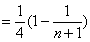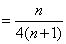- 数列的概念与简单表示法
- 共1089题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
现有一组互不相同且从小到大排列的数据

记



(1)求

(2)设直线


(3)证明:当

正确答案
见解析
解析
(1)解:

(2)解:

因为 
所以 
(3)证:由于



事实上,当

下面证明
法一:对任何



所以 
法二:对任何
当

当
综上,
知识点
已知等差数列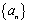
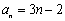
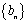
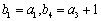
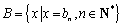
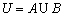
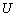
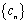
(1)求数列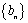
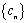
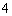
(2)把集合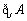
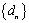
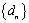
(3)求数列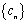
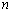
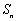
正确答案
见解析
解析
(1)解:设等比数列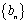
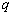

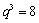
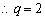
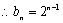
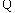
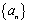
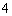
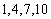

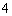
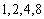


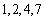
(2)解:据集合
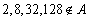

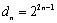
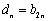

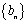
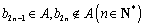
证明如下:
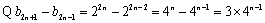
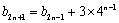
若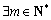
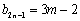
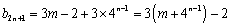
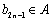
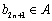
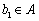
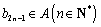
同理,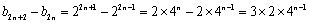
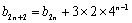
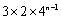
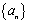
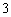
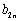
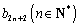
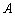
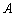
当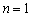
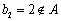
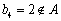
即得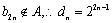
(3)解:(1)当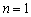
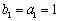
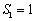
(2)当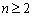

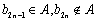
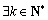
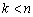
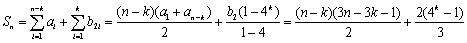
下面讨论正整数
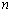
数列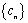
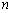
①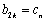
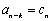
若①成立,即有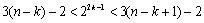
若②成立,即有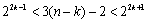

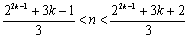
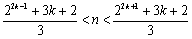
显然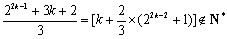
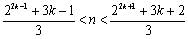
综上所述,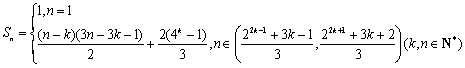
知识点
将数列{
……
已知表中的第一列数






(1)求数列{
(2)若上表中从第2行开始,每一行中的数按从左到右的顺序均成等比数列,且公比是同一个正数,已知

正确答案
见解析。
解析
知识点
设满足以下两个条件的有穷数列
① 
② 
(1)分别写出一个单调递增的3阶和4阶“期待数列”;
(2)若某2k+1(
(3)记n阶“期待数列”的前k项和为

正确答案
见解析
解析
(1)数列
数列
(2)设等差数列




即

当d=0时,与期待数列的条件①②矛盾, ……………………………………………………5分
当d>0时,据期待数列的条件①②得:
由


当d<0时,
同理可得
由


(3)(i)当k=n时,显然
当k<n时,据条件①得

即


(ii)

知识点
已知等差数列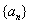
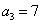
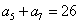
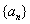
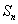
(1) 求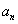
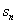
(2) 令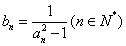
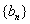
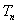
正确答案
见解析。
解析
(1)设等差数列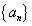
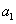
由于
所以
解得
由于
(2)因为 
因此
故
所以数列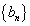
知识点
对数列


成立,其中


①若


②若


③若数列



其中,正确结论的个数是( )。
正确答案
解析
略
知识点
(1)设

(2)

正确答案
见解析
解析
本题考查不等式的性质,对数函数的性质和对数换底公式等基本知识,考查代数式的恒等变形和推理论证能力。
证明:(1)由于x≥1,y≥1,所以
将上式中的右式减左式,得
既然x≥1,y≥1,所以
(2)设
于是,所要证明的不等式即为
其中
故由(1)立知所要证明的不等式成立。
知识点
已知数列






(1)求
(2)求证:在数列


(3)求数列
正确答案
见解析。
解析
(1) 
(2) ① 任意


② 假设
∴ 在数列


(3) 


∵
知识点
在等差数列{an}中,a2=5,a1+a4=12,则an= ;设
正确答案
2n+1;
解析
设等差数列{an}的公差为d,则由a2=5,a1+a4=12 可得 

故an=3+(n﹣1)2=2n+1。
∵ 




∴ 数列{bn}的前n项和Sn=





知识点
扫码查看完整答案与解析