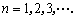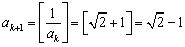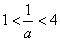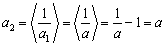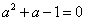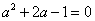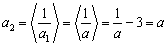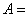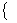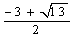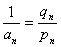- 数列的概念与简单表示法
- 共1089题
已知数列





正确答案
解析
略
知识点
已知函数


(1)求函数
(2)若关于


(3)数列


求
正确答案
见解析。
解析
(1)由f(x)=a x2+bx+1,所以f′(x)=2ax+b,
因为函数f(x)=a x2+bx+1在x=3处的切线方程为y=5x﹣8,所以切点为(3,7)。
则
所以f(x)=x2﹣x+1;
(2)由(1)知f(x)=x2﹣x+1,
关于x的方程f(x)=kex恰有两个不同的实根,
即x2﹣x+1=k•ex有两个不同的实根,也就是k=e﹣x(x2﹣x+1)有两个不同的实根。
令g(x)=e﹣x(x2﹣x+1),
则g′(x)=(2x﹣1)e﹣x﹣(x2﹣x+1)e﹣x
=﹣(x2﹣3x+2)e﹣x=﹣(x﹣1)(x﹣2)e﹣x
由g′(x)=0,得x1=1,x2=2。
所以当x∈(﹣∞,1)时,g′(x)<0,g(x)在(﹣∞,1)上为减函数;
当x∈(1,2)时,g′(x)>0,g(x)在(1,2)上为增函数;
当x∈(2,+∞)时,g′(x)<0,g(x)在(2,+∞)上为减函数;
所以,当x=1时,g(x)取得极小值g(1)=

函数y=k与y=g(x)的图象的大致形状如下,
由图象可知,当k=

(3)由2a1=f(2)=22﹣2+1=3,所以


又
所以an+1>an>1。
又
则

所以
=
=


又S=
故
知识点
已知数列




(1) 求数列
(2)若


正确答案
见解析。
解析
(1) 解:
∴ 当


由
得
② - ①得: 
以下提供两种方法:
法1:由③式得:
即

∵
∴数列
∴

当

又
∴
法2:由③式得:
得
当

⑤-④得:
由

∴
∴数列


(2)解:∵
∴
假设
则
即
化简得:
∵
∴
∴
知识点
对于实数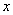
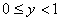
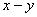
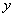
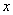
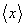
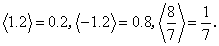
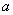
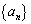
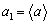
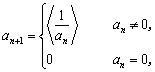
(1)若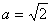
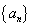
(2)当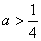

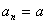
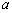
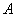
(3)若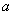
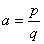
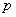
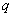
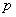
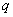
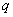
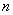
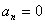
正确答案
见解析
解析
(1)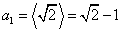
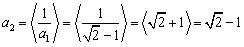
若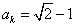
所以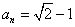
(2)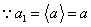
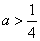
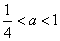
①当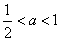
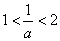
所以
解得: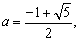
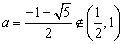
②当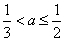
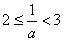
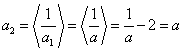
所以
解得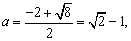
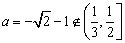
① 当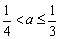

解得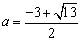
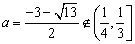
综上,集合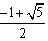
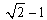
(3)结论成立. ……………………8分
由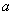
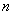
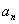
可设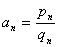
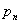
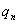
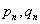
由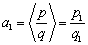
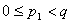
若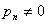
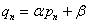
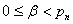
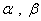
则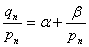
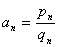
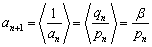
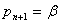
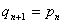
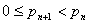
若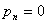
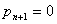

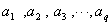
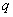
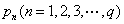
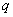
但小于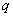
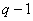
故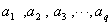
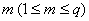

从而数列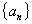
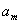
所以对于大于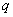
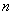

知识点
已知数列





则
正确答案
解析
略
知识点
已知数列




(1)求数列
(2)设数列



(3)在第(2)问的条件下,若对于任意的


正确答案
(1)
(2)
(3)
解析
(1)由题意可知,
当

当

所以
(2)由(1)可知

当

当


当

当


……
当



以上

又


同理,当

所以,当

因此,当



当



故数列


(3)由(2)可知
①当

所以




②当

所以


综上,
因此,若对于任意的


故实数

知识点
已知


正确答案
-1/2
解析
略
知识点
若对于正整数





(1)求

(2)求


(3)求数列
正确答案
见解析
解析
(1)

(2)


(3)由(1)(2)不难发现对

所以当

于是

所以


又
所以对

知识点
对于数列



列








(1)试问



(2)求

(3)证明:

正确答案
见解析
解析
(1)解:数列







数列




(2)解:


若


当数列



当

由数列



为常数列。
其它情形同理,得证。
在数列



所以,数列


(3)证明:先证明引理:“数列


证明:记数列


令


因为

故
现将数列
第一类是没有为


第二类是含有为

下面证明第二类数列

不妨令数列



① 当数列

若


或含有
若

此数列各项均不为

若



类数列;
若



此数列各项均不为
② 当数列




各项均不为
若



各项均不为

③ 当数列






总之,第二类数列




又因为各数列的最大项是非负整数,
故经过有限次“


知识点
一个三角形数表按如下方式构成(如图:其中项数




(1)求第2行和第3行的通项公式

(2)证明:数表中除最后2行外每一行的数都依次成等差数列,并求


(3)若







正确答案
见解析
解析
(1)

(2)由已知,第一行是等差数列,假设第

则由



由于



得
于是
即





(3)

令




令




知识点
扫码查看完整答案与解析