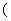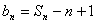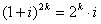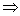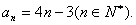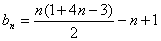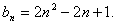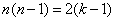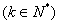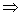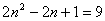- 数列的概念与简单表示法
- 共1089题
8.数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
定义“等和数列”:在一个数列中,如果每一项与它的后一项的和为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列



正确答案
解析
略
知识点
数列{an}的项是由l或2构成,且首项为1,在第k个l和第k+1个l之间有2k﹣1 个2,即数列{an} 为:1,2,1,2,2,2,1,2,2,2,2,2,1,…,记数列 {an}的前n项和为Sn,则S20= ; S2013= 。
正确答案
36,3981
解析
设f(k)=2k﹣1,则数列为1,2,1,2,2,2,1,2,2,2,2,2,1…
∴前20 项中共有16个24个1
s20=1×4+2×16=36
记第k个1与其后面的k个2组成第k组,其组内元素个数记为bk,则bk=2k
b1+b2+…+bn=2+4+…+2n=n(n+1)<2013,
而46×45=2080<2011,47×46=2162>2013
故n=45即前2011项中有45个1以及1968个2,所以S2013=45+1968×2=3981
故答案为:36,3981
知识点
已知每项均是正整数的数列




(1)设数列

(2)若

(3)若

正确答案
见解析
解析
(1)因为数列
所以
所以
(2) 一方面,
根据

故

当且仅当
因为


所以
即当



(3)设

由(2)可以知道,

根据题意,
下面计算

∵

∴

知识点
数列{an}的通项公式an=ncos
正确答案
3018
解析
因为cos
∴ncos
∴ncos
∴数列{an}的每四项和为:2+4=6。
而2012÷4=503;
∴S2012=503×6=3018。
知识点
已知数列





正确答案
解析
略
知识点
由等式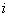
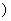
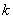
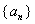
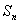
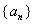
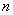
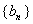
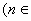
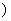
(1)试求数列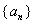
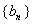
(2)若甲数列的每一项都是乙数列的项,且乙数列中至少有一项不是甲数列的项,则称甲数列是乙数列的真子数列.试证明:数列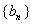
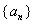
正确答案
见解析
解析
(1)解:由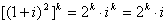
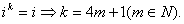
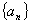
由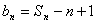
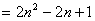
(2)即对任意的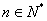
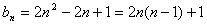
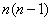
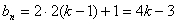
这表明对任意的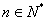
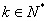
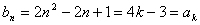
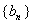
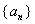
而对于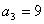
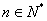
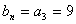
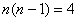
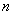
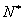

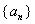
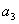
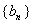
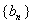
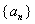
知识点
已知向量







正确答案
解析
略
知识点
10.试在无穷等比数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析