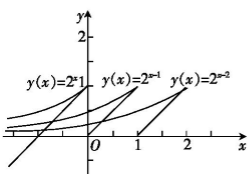- 数列的概念与简单表示法
- 共1089题
5.南宋孝宗淳熙二年(1175),朱(朱熹)陆(陆九渊)“鹅湖之会”开启了“朱陆异同”的争辩,其共同主旨包括:( )
①道问学
②植纲常
③扶名教
④宗孔孟
正确答案
解析
此题是比较型选择题。根据所学知识,我们知道朱熹陆象山都是南宋同时代的理学家,他们哲学核心都是“理”,在朱为“性”,在陆为“心”,派生万物,或统一万物,因而都是精神第一性,物质第二性,颠倒了哲学的根本问题。他们夸大了“精神”的绝对作用,实质上成了“虚构的神学”,把人们引向僧侣主义。他们在政治上都是同植纲常,同扶名教,同宗孔孟,同为中国封建专制政权服务。所以正确答案选择B项。道问学是朱熹的观点,属于二者的分歧,故应排除。
考查方向
解题思路
此题是比较型选择题。根据所学知识,我们知道朱熹陆象山都是南宋同时代的理学家,他们哲学核心都是“理”,在朱为“性”,在陆为“心”,派生万物,或统一万物,因而都是精神第一性,物质第二性,颠倒了哲学的根本问题。他们夸大了“精神”的绝对作用,实质上成了“虚构的神学”,把人们引向僧侣主义。他们在政治上都是同植纲常,同扶名教,同宗孔孟,同为中国封建专制政权服务。所以正确答案选择B项。二者的区别主要表现在一下方面:在认识论上——朱熹主张“性即是理”,陆象山主张“心即是理”。在方法论上——朱熹主张“道问学”,从外而内,陆象山主张“尊德性”,从内而外。在宇宙观上——朱熹坚持“无极而太极”;陆象山则认为“易有太极”,“太极”之上不能加“无极”二字。在历史观上——朱熹主张“陶铸历史,会归一理的纯粹”;陆象山则认为:“先王之泽竭,此心放失陷溺而然也。”
易错点
此题出错点在于概念混淆而出错。
知识点
已知数列


22. 求q的值和
23. 设


正确答案
(I) 
解析
(I) 由已知,有

所以




当

当

所以
考查方向
解题思路
(I)由



易错点
不会讨论来解答。
正确答案
(II) 
解析
(II)解:由(I)得




上述两式相减,得

整理得,
所以,数列


考查方向
解题思路
(II)求出数列
易错点
没有掌握求和方法。
设等差数列{an}的前n项和为Sn,且S4=4S2,a2n=2an+1.
17.求数列{an}的通项公式;
正确答案
见解析
解析
考查方向
解题思路
第1问,根据Sn和an的关系判断出数列为等差数列,根据等比数列通项公式求通项,第2问结合第1问得到的结论,得到Bn的通项,进而求出bn的前n项和。
易错点
求数列通项公式错误
正确答案
见解析
解析
考查方向
解题思路
第1问,根据Sn和an的关系判断出数列为等差数列,根据等比数列通项公式求通项,第2问结合第1问得到的结论,得到Bn的通项,进而求出bn的前n项和。
易错点
求数列通项公式错误
设数列



16.求数列
17.记数列


正确答案
解析
由已知

即
从而
又因为

所以

所以,数列
故
考查方向
解题思路
利用





易错点
不会根据Sn=2an-a3求出an=2an-1(n≥2);
正确答案
10.
解析
由(1)得
所以
由

因为
所以
于是,使
考查方向
解题思路
由(1)得



易错点
求前n项和时对于项数出错。
12.在数列{an}中,a1=3, an=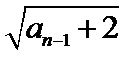
正确答案
解析
由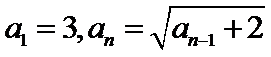
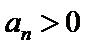
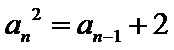
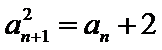
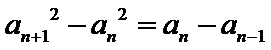
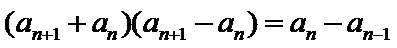
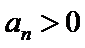
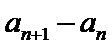
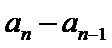
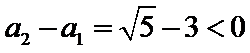
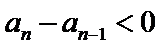
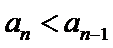
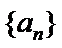
考查方向
解题思路
先对an=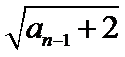
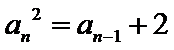
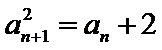
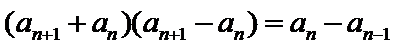
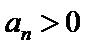
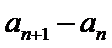
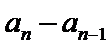
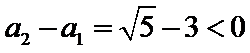
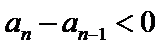
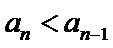
故B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
转化条件an=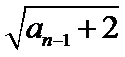
知识点
已知正项数列




22.求

23.是否存在非零整数
对一切

正确答案

解析
解:由.
当



当
由
∵


∴

另法:易得



考查方向
解题思路
利用数列前


另法:易得



易错点
利用数列前


正确答案
存在
解析
由

设


∵


假设存在这样的实数


① 当

② 当


综上,


考查方向
解题思路
先进行化简转化




易错点
利用数列前


已知数列

24.若

25.若



正确答案
见解析
解析
(1)
当
当
考查方向
解题思路
由数列

易错点
主要易错于递推关系找不出,
正确答案
见解析
解析
(2)方法1:

①/②得,因为
方法2:因为
又因为
所以

所以

所以:
考查方向
解题思路
这里可以从两个方面进行分析
①直接找出
②根据递推关系得出
易错点
主要易错于递推关系找不出,
已知






22.求数列

23.设






正确答案
(1)
解析
(1)因为

所以



所以
考查方向
解题思路
1.第(1)问根据等差数列、等比数列的基本量求出通项公式;2.根据第(1)问求出
易错点
1.不会将


正确答案
(1)
解析
(2)

所以

(或
因为



所以,不存在正整数

考查方向
解题思路
1.第(1)问根据等差数列、等比数列的基本量求出通项公式;2.根据第(1)问求出
易错点
1.不会将


已知


17.求数列
18.求数列


正确答案
(1)
解析
(1) 设



由


考查方向
解题思路
利用等差数列的性质求出数列
易错点
利用等差数列的性质求通项公式和等比数列的性质混淆;
正确答案
解析
(2)
由
得
① -②得

又
当


考查方向
解题思路
根据公式构造等式求出
易错点
先构造等式做差后求出
6.已知函数f(x)=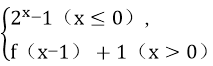
正确答案
解析
当x∈(-∞,0]时,由g(x)=f(x)-x=2x-1-x=0,得2x=x+1.令y=2x,y=x+1.在同一个坐标系内作出两函数在区间(-∞,0]上的图象,如图,
由图象易知交点为(0,1),故得到函数的零点为x=0.
当x∈(0,1]时,x-1∈(-1,0],f(x)=f(x-1)+1=2x-1-1+1=2x-1,由g(x)=f(x)-x=2x-1-x=0,得2x-1=x.令y=2x-1,y=x.在同一个坐标系内作出两函数在区间(0,1]上的图象,由图象易知交点为(1,1),故得到函数的零点为x=1.
当x∈(1,2]时,x-1∈(0,1],f(x)=f(x-1)+1=2x-1-1+1=2x-2+1,由g(x)=f(x)-x=2x-2+1-x=0,得2x-2=x-1.令y=2x-2,y=x-1.在同一个坐标系内作出两函数在区间(1,2]上的图象,由图象易知交点为(2,1),故得到函数的零点为x=2.
依此类推,当x∈(2,3],x∈(3,4],…,x∈(n,n+1]时,构造的两函数图象的交点依次为(3,1),(4,1),…,(n+1,1),得对应的零点分别为x=3,x=4,…,x=n+1.
故所有的零点从小到大依次排列为0,1,2,…,n+1.其对应的数列的通项公式为an=n-1.
知识点
扫码查看完整答案与解析