- 数列的概念与简单表示法
- 共1089题
已知数列{an}的前n项和sn满足:sn+sm=sn+m,且a1=1,那么a10=
正确答案
解析
根据题意,在sn+sm=sn+m中,
令n=1,m=9可得:s1+s9=s10,即s10﹣s9=s1=a1=1,
根据数列的性质,有a10=s10﹣s9,即a10=1。
知识点
已知正项等比数列{an}满足:a3=a2+2a1,若存在两项am,an,使得

正确答案
解析
∵正项等比数列{an}满足:a3=a2+2a1,
∴
即:q2=q+2,解得q=﹣1(舍),或q=2,
∵存在两项am,an,使得
∴
∴
∴
所以,m+n=6,
∴








所以,

知识点
已知
(1)求数列
(2)设数列


正确答案
(1)
解析
解析:(1)设等比数列


又∵


∴
(2)由题意可得 


两式相减得 
∴

当

∴

∴
知识点
数列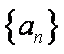
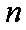
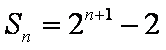
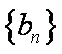
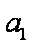
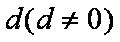
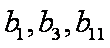
(1)求数列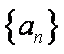
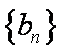
(2)设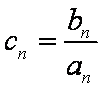
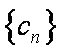
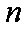
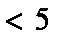
正确答案
见解析
解析
(1)当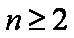
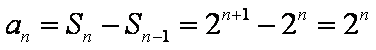
又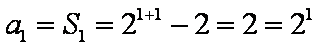
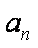
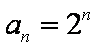
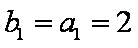
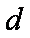
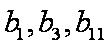
得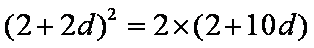
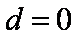
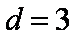
所以数列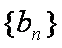
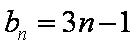
(2)由(1)可得
知识点
已知数列{an}满足
(1)求证:数列{an+1﹣an}是等比数列,并求{an}的通项公式;
(2)记数列{an}的前n项和Sn,求使得Sn>21﹣2n成立的最小整数n。
正确答案
见解析。
解析
(1)证明:
∴an+2﹣an+1=2(an+1﹣an),a2﹣a1=3
∴数列{an+1﹣an}是以3为首项,公比为2的等比数列,
∴an+1﹣an=3•2n﹣1(3分)
∴n≥2时,
an﹣an﹣1=3•2n﹣2,
…
a3﹣a2=3•2,
a2﹣a1=3,
以上n﹣1个式子累加得an﹣a1=3•2n﹣2+3•2n﹣3+…+3•2+3=3(2n﹣1﹣1)
∴an=3•2n﹣1﹣2
当n=1时,
从而可得
(2)解:由(1)利用分组求和法得
Sn=(3•20﹣2)+(3•21﹣2)+…(3•2n﹣1﹣2)
=3(20+21+…+2n﹣1)﹣2n
=
=3(2n﹣1)﹣2n(9分)
Sn=3(2n﹣1)﹣2n>21﹣2n,
得3•2n>24,即2n>8=23,
∴n>3
∴使得Sn>21﹣2n成立的最小整数4.(12分)
知识点
等比数列{an}的各项均为正数,且a5a6+a4a7=18,则log3a1+log3a2+…log3a10=
正确答案
解析
∵a5a6=a4a7,
∴a5a6+a4a7=2a5a6=18
∴a5a6=9
∴log3a1+log3a2+…log3a10=log3(a5a6)5=5log39=10
知识点
已知数列{an}中
正确答案
解析
∵数列{an}中
∴an+1﹣an>0对于n∈N*恒成立即(n+1)2﹣k(n+1)﹣(n2﹣kn)=2n+1﹣k>0对于n∈N*恒成立,
∴k<2n+1对于n∈N*恒成立,即k<3。
知识点
定义:在数列



差比数列”。已知在“等差比数列”

正确答案
解析
略
知识点
已知变量x,y满足约束条件


正确答案
解析
易知
设


当



当




由



知识点
已知等差数列{an}的公差为2,若a1,a3,a4成等比数列,则a2=
正确答案
-6
解析
由等差数列{an}的公差为2,得到a3=a1+4,a4=a1+6,
又a1,a3,a4成等比数列,
∴(a1+4)2=a1•(a1+6),
解得:a1=-8,
则a2=a1+d=-8+2=-6。
知识点
扫码查看完整答案与解析