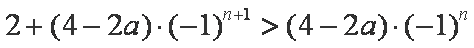- 数列的概念与简单表示法
- 共1089题
已知公差不为0的等差数列{an}的前n项和为Sn,S3=a4+6,且a1,a4,a13成等比数列。
(1)求数列{an}的通项公式;
(2)设bn=2an+1,求数列{bn}的前n项和。
正确答案
见解析
解析
(1)设等差数列

因为

因为

由①,②可得:
所以
(2)由题意





所以数列


所以
知识点
数列{an}的前n项和为Sn,且Sn=

(1)求数列{an}与{bn}的通项公式。
(2)设数列{cn}满足cn = an log2 (bn+1),其前n项和为Tn 求Tn。
正确答案
(1)an=3n,bn=42-n-1
解析
(1) 对于数列


由①-②得




则
对于数列





(2)由(1)可知:
(8分)


由③-④得

则
知识点
已知等比数列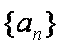
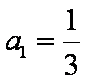
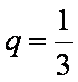
(1)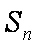
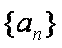
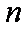

(2)若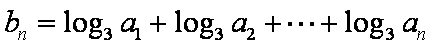
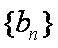
正确答案
见解析。
解析
(1)∵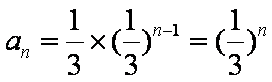


(2)bn=log3a1+log3a2+……+log3an=(1+2+……+n)=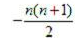
∴数列{bn}的通项公式为bn=
知识点
设等比数列{





(1)求r的值;
(2)记

正确答案
(1)r=-1(2)Tn=
解析
(1)依题
当

当

又因为{

所

(1)另解:
当

当

∴
∵ {


(2)由(1)
∴ 
即 
所以 
知识点
设


正确答案
解析
略
知识点
已知数列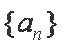
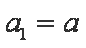
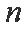
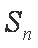
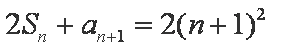
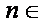
(1)求数列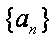
(2)对任意的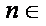
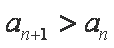
正确答案
见解析
解析
(1)由条件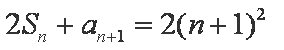
两式相减得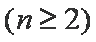
故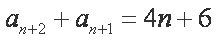
两式再相减得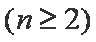
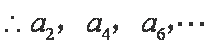
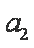
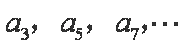
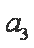
又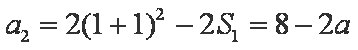
所以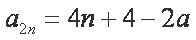
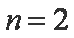
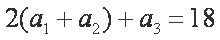
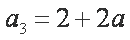
从而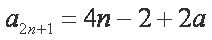
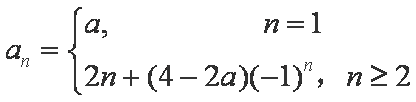
(2)对任意的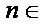
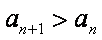
当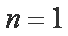
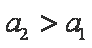
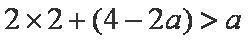
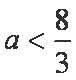
当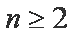
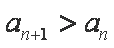
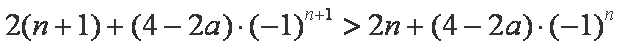
即
若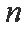
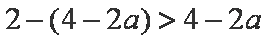
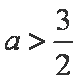
若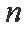
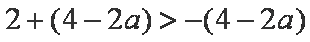
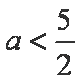
由①、②、③得: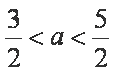
知识点
已知函数








(1)求
(2)求证:

(3)设




正确答案
见解析。
解析
(1)易知


即
∴
(2)构造函数

则
即函数

∴

∴当


∴知
∴

(3)

∴当



当


方法二:
(1)(2)同方法一;
(3)由(2)知



又

∴综上所述:对一切


知识点
在等差数列{an}中,已知a4+a8=16,则该数列前11项和S11=
正确答案
解析
在等差数列中,
知识点
已知等比数列{an}为递增数列,且
通项公式an =______________。
正确答案
解析
知识点
已知数列






正确答案
解析
略
知识点
扫码查看完整答案与解析