- 数列的概念与简单表示法
- 共1089题
3.等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.等差数列{an}的前n项和为Sn,且a1>0,若存在自然数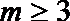
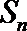
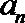
正确答案
<
解析
解析已在路上飞奔,马上就到!
知识点
14.某纺织厂的一个车间有n(n>7,n∈N)台织布机,编号分别为1,2,3,……,n,该车间有技术工人n名,编号分别为1,2,3,……,n.现定义记号




正确答案
1;第3名工人操作了两台织布机
解析
解析已在路上飞奔,马上就到!
知识点
9. 已知数列



正确答案
18
解析
解析已在路上飞奔,马上就到!
知识点
19.设数列



(1)求数


(2)若


正确答案
(1)数列
所
又因为
由
n=1时,

所以

(2)由(1)知,

=
=1-4+
解析
解析已在路上飞奔,马上就到!
知识点
5.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知



(1)求数列
(2)设数列


正确答案
(1)
(2)设
=
因为 
解析
解析已在路上飞奔,马上就到!
知识点
6.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知等差数列




(1)求数列
(2)若将数列












正确答案
(1)
(2)由题意得:
而
是首项为


所以
所以
所以
所以
解析
解析已在路上飞奔,马上就到!
知识点
4.等差数列{an}的前n项和为Sn,若a1=2,S3=12,则a6等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析










































