- 数列的概念与简单表示法
- 共1089题
22.可以证明, 对任意的

(1) 设由三项组成的数列


(2) 设数列







(3) 是否存在满足(2)中条



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知等差数列




(1)求
(2)若



正确答案
(1)设数列


由题意可求得

(2)

解析
解析已在路上飞奔,马上就到!
知识点
12.已知数列







正确答案
8或9
解析
解析已在路上飞奔,马上就到!
知识点
18.设等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列{an}满足:

(Ⅰ)求
(Ⅱ)记数列{an}前2n项和为


正确答案
(I)∵ a1=20,a2=7,an+2﹣an=﹣2 ∴ a3=18,a4=5
由题意可得数列{an}奇数项、偶数项分布是以﹣2为公差的等差数列
当n为奇数时,
当n为偶数时,
∴ an=
(II)s2n=a1+a2+…+a2n =(a1+a3+…+a2n﹣1)+(a2+…+a2n)
=
结合二次函数的性质可知,当n=7时最大
解析
解析已在路上飞奔,马上就到!
知识点
9.数列

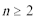
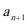


正确答案
9
解析
解析已在路上飞奔,马上就到!
知识点
6.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知等比数列







(1)证明:
(2)求

(3)证明:若数列


正确答案
(1)
当
同理
当
(2)
又


当




又因为
∴


又因为
因此当

(3)



①当

则
因此
公差
②当
设
则
∴
因此
公差
综上可知,
且
∴数列
解析
解析已在路上飞奔,马上就到!
知识点
3.在等比数列
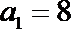
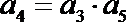
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列


(1)记


(2)求
(3)当


正确答案
(1)由
得
即
又
所以

所以

(2)由

=
当
当
(3)由
知
=
因为
所以
则
又
所以
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析

























































