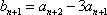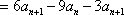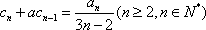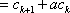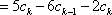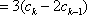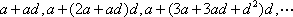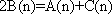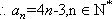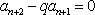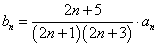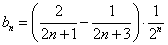- 数列的概念与简单表示法
- 共1089题
设数列



(1)证明数列
(2)证明:对任意

(3)对于(2)中的命题,对一般的各项均为正数的等差数列还成立吗?如果成立,请证明你的结论,如果不成立,请说明理由。
正确答案
见解析
解析
解析:(1)∵


两式相减得
∴
∵

又
∴


∴
(2)由(1)知
∴
于是

∴

(3
设等差



于是

将

∴
又

∴
知识点
已知等比数列






(1)求数列




正确答案
见解析
解析
解:(1)设数列

若






由



即

(2)由(1)得,
所以
知识点
已知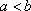
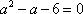
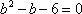
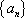
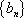
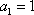
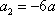
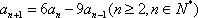
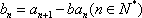
(1) 求证数列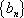
(2) (理科)求数列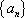
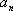
(3) (理科)若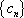
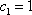
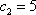
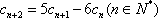
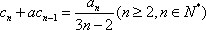
正确答案
见解析
解析
(1)∵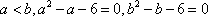
∴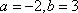
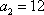
∵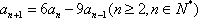
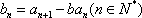
∴
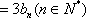
又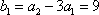
∴数列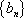
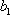
(2)依据(1)可以,得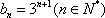
于是,有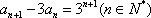
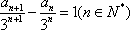
因此,数列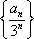
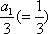
故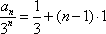
所以数列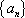
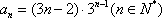
(3)用数学归纳法证明:
(i)当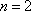
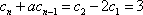
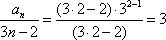
即左边=右边,所以当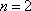
(ii)假设当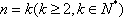
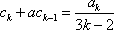
当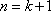
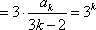
右边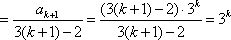
即左边=右边,因此,当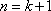
根据(i)、(ii)可以断定,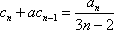
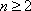
所以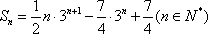
知识点
对于数列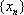

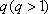
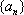
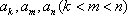
(1)若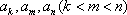
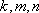
(2)他猜想:“在上述数列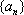
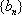
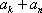
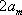
(3)他又想:在首项为正整数
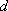
正确答案
见解析
解析
解析:(1)由已知可得: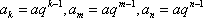
则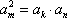
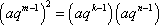
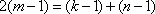
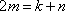
(2) 
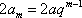
故 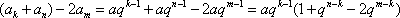
由于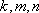
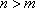
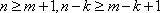
又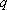
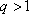
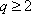
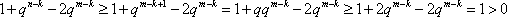
所以,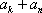
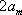
(3)命题:对于首项为正整数
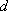
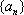
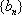
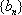
此命题是真命题,下面我们给出证明.
证法一: 只

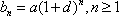
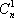
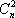
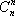
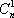
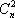
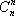
证法二:首项为
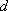
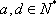
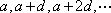
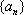
依次取数列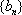
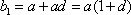
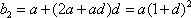
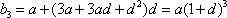
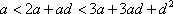
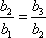
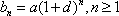
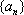
知识点
在平面直角坐标系上,设不等式组



(1)求数列
(2)若



正确答案
见解析。
解析
(1)由

所以平面区域为

直线



(2)由

知识点
已知函数









(1)若k=1,求数列
(2)若m=2,问是否存在常数


(3)若

正确答案
见解析
解析
解析:(1)因为
所以其值域为
于是
又
(2)因为
所以
法一:假设存在常数
使得数列
得
法二:假设存在常数k>0,使得数列


当
则
(3)因为


于是
则

因此

又

进而有
知识点
已知数列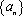
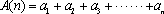
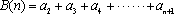
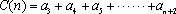
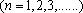
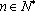
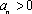
(1)若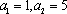
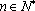
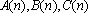
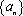
(2)证明:数列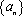
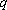
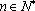
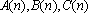
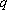
正确答案
见解析
解析
解析:(1)
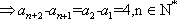
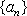
(2)(必
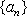
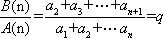
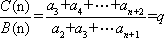
(充分性):若对于任意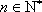
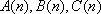
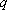
则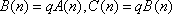
于是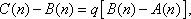
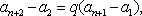
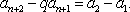
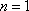
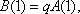
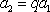
因为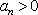
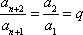
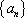
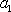
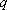
综上,数列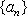
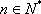

知识点
定义数列







(1) 写出数列
(2) 设


(3)求
正确答案
见解析
解析
解析:解:(1)由题设,满足条件的数列
(1)


(3)

(5)

2个起评,对2个1分,3个2分,4个3分,5个4分,6个5分
(2)

则





…

所以
因为






所以

(3)
则当





此时
证明如下:
假设













所以 


所以
知识点
等比数列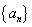
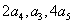
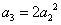
(1)求数列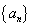
(2)设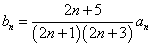
正确答案
见解析
解析
(1)解: 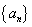
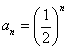

(2)解:由(1),得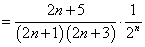
所以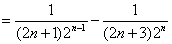
所以
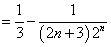
故数列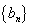
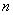
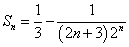
知识点
在数列

(1)数列


(2)数列


正确答案
(1)
解析
法1:
法2:
(1)
(2)
知识点
扫码查看完整答案与解析