- 数列的概念与简单表示法
- 共1089题
设等差数列





(1)求
(2)若数列



正确答案
见解析。
解析
解析:(1)设数列






(2)由
知
两式相减:

当

即
知识点
已知数列



(1)求数列

(2)设



正确答案
见解析。
解析
(1)


令


因此,数列




(2)(方法一)先证明当

设









因此,当


当




(方法二)数学归纳法证明
(1)






又




(2)设


当

要证

化简,即证
设









因此,不等式


当

要证

化简,即证
根据前面的证明,不等式


由数学归纳法可知,当


知识点
已知数列


(1)求常数p的值和数列
(2)若抽去数列


(3) 在(2)的条件下,设数列


正确答案
见解析
解析
(1)解:由


又因为存在常数

则


故数列

此时


(2)解:由等比数列的性质得:
(i)当

(ii) 当

所以
(3)解:注意到





(i)当

(ii)当

即
知识点
已知






(1)求数列


(2) 如果对于


正确答案
见解析
解析
(1)由已知有

所以

所以
因为

(2)




所以

即


而



知识点
对数列





(1)设数列



(2)设数列


(3)设数列





正确答案
见解析
解析
(1)
(2)




因此,

所以,


(3)

不等式为


设

……………15分
当






知识点
已知等差数列



(1)求数列

(2)设数列



正确答案
见解析。
解析
(1)由已知得


所以


又因为

所以
又



所以
(2)由


①-②,得当


而



所以

知识点
已知数列




(1)求通项公式
(2)设






正确答案
见解析。
解析
(1)当



所以,当



又









所以,
(2)由(1),得


所以,若存在正整数



显然,当

当


显然,当

当

所以
当

当


所以
综上所述,所有的符合条件的正整数对


知识点
设数列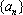
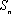
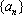
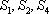
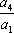
正确答案
解析
由
知识点
如果存在常数







(1)若数列:



(2)已知有穷等差数列





(3)对于一个不少于3项,且各项皆为正整数的递增数列
正确答案
见解析
解析
(1)因为数列:

所以

故
即
(2)设数列



若
即对数列

同理可得:若

由“兑换数列”的定义可知,数列
又因为数列



(3)假设存在这样的等比数列

因为数列
则
又因为数列


故数列

则
①若




②若

即


综合①②得,不存在满足条件的数列
知识点
设曲线






(1)求数列
(2)求证:
(3)是否存在常数


正确答案
见解析。
解析
(1)设点


因为




又

将

两边平方得

故数列



因为

(2)因为
所以
所以
以上

(3)因为


因为
所以
所以
所以
故存在常数


知识点
扫码查看完整答案与解析