- 数列的概念与简单表示法
- 共1089题
12.数列



正确答案
解析
假设
∵
∴






知识点
2.已知各项均为正数的等比数列{


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.各项为正数的数列

(1)求
(2)设函数
正确答案
(1)由
当n≥2时,
由①-②化简得:

又∵数列
∴当n≥2时,

故数列
又
解得
(2)由分段函数
可以得到:

当n≥3,

解析
解析已在路上飞奔,马上就到!
知识点
7.已知等比数列{an}的各项都为正数,它的前三项依次为1,a+1,2a+5,则数列{an}的通项公式
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知等差数列{an}和正项等比数列{bn},a1=b1=1,a3=b3=2。
(1)求an,bn;
(2)设
(3)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列{an}的前n项和为Sn,且满足an=
(1)求数列{an}的通项公式;
(2)若


正确答案
(1) an=
an-1=
①-②得:an=2an-1(n≥2),
又易得a1=2
∴ an=2n
(2) bn=n,
裂项相消可得
∵
∴ 欲
须
又k正整数,
∴ k=5、6、7
解析
解析已在路上飞奔,马上就到!
知识点
14.已知f(x)是定义在R上不恒为零的函数,对于任意的x,y∈R,都有f(x·y)=xf(y)+yf(x)成立。数列{an}满足an=f(2n)(n∈N*),且a1=2。则数列的通项公式an=( )
正确答案
n·2n
解析
由an+1=f(2n+1)=2f(2n)+2nf(2)=2an+2n+1,得


知识点
20.记数列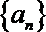
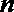
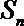
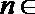
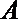
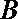
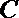
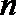
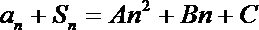
(1)已知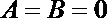
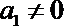
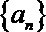
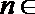
(2)已知数列
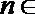
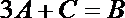
(3)已知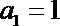
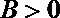
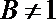
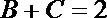
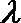

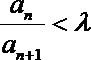
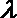
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某同学五次测验的成绩分别为78,92,86,84,85,则该同学五次测验成绩的方差为( )
正确答案
20
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析






















