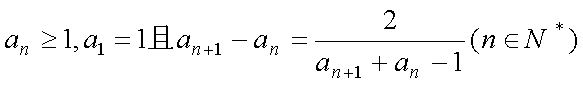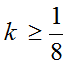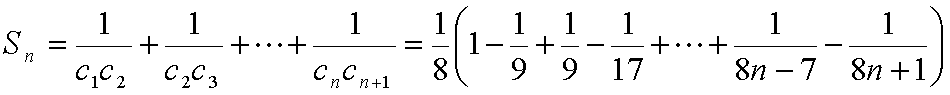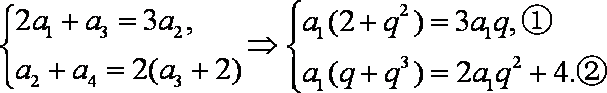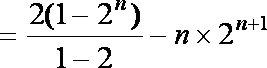- 数列的概念与简单表示法
- 共1089题
已知点(1,
















(2)若数列




(3)若数列{




正确答案
(1)

解析
解析:(1)



又数列


又公比



又


数列

当




(2)


①式减②式得:

化简:
所以所求
(3)


由


知识点
已知



正确答案
见解析
解析
由题意可得
又∵
=








知识点
设Sn=





(1)证明:当n∈N*,n≥2时,Sn+1=Sn﹣Sn﹣1;
(2)记S=




正确答案
见解析。
解析
(1)当n为奇数时,n+1为偶数,n﹣1为偶数,
∵
Sn=

Sn﹣1=

Sn+1﹣Sn=﹣(

当n为奇数时,Sn+1=Sn﹣Sn﹣1成立,
同理可证,当n偶数时,Sn+1=Sn﹣Sn﹣1也成立,
(2)由S=




2014S=




=








=(




=S2014﹣S2012,
又由,Sn+1=Sn﹣Sn﹣1得Sn+6=Sn。
∴S2014﹣S2012=S4﹣S2=﹣1,
∴
知识点
在数列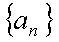
(1)求数列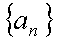
(2)令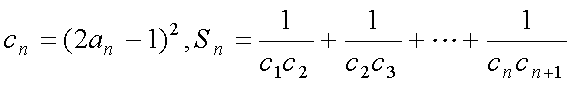
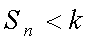
正确答案
(1)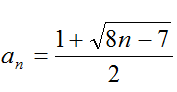
解析
解析:(1)解:因为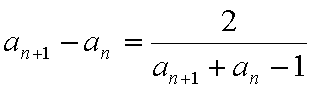
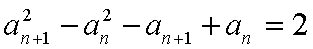
即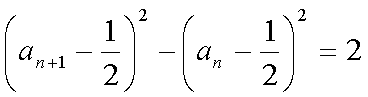
令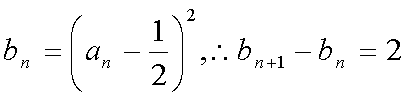
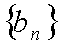
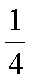
所以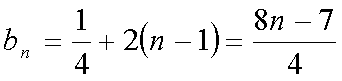
因为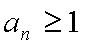
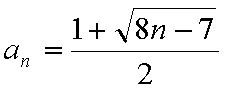
(2)因为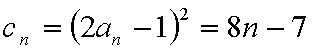
所以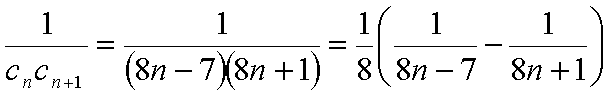
所以
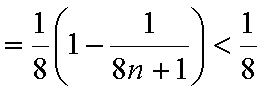
因为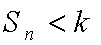
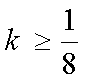
知识点
数列












(1)求数列

(2)比较




正确答案
(1)

解析
解析:(1)由题意
解得

又

解得


(2)由(1)知
∴
又
∴
由①②可知
知识点
已知数列{an}的通项公式为an=﹣n+p,数列{bn}的通项公式为bn=2n﹣5,设cn=
正确答案
(12,17)
解析
当an≤bn时,cn=an,当an>bn时,cn=bn,∴cn是an,bn中的较小者,
因为an=﹣n+p,所以{an}是递减数列;因为bn=2n﹣5,所以{bn}是递增数列,
因为c8>cn(n≠8),所以c8是cn的最大者,
则n=1,2,3,…7,8时,cn递增,n=8,9,10,…时,cn递减,
因此,n=1,2,3,…7时,2n﹣5<﹣n+p总成立,
当n=7时,27﹣5<﹣7+p,∴p>11,
n=9,10,11,…时,2n﹣5>﹣n+p总成立,
当n=9时,29﹣5>﹣9+p,成立,∴p<25,
而c8=a8或c8=b8,
若a8≤b8,即23≥p﹣8,所以p≤16,
则c8=a8=p﹣8,
∴p﹣8>b7=27﹣5,∴p>12,
故12<p≤16,
若a8>b8,即p﹣8>28﹣5,所以p>16,
∴c8=b8=23,
那么c8>c9=a9,即8>p﹣9,
∴p<17,
故16<p<17,
综上,12<p<17。
知识点
记等差数列{an}的前n项和为Sn。
(1)求证:数列{
(2)若a1=1,且对任意正整数n,k(n>k),都有


(3)记bn=


正确答案
见解析
解析
设等差数列{an}的公差为d,
(1)由于

所以当n≥2时,

即数列{
(2)∵对任意正整数n,k(n>k),都有


∴

则

所以当n≥2时,an=Sn﹣Sn﹣1=[1+(n﹣1)t]2﹣[1+(n﹣2)t]2=2t2n﹣3t2+2t,
又由等差数列{an}中,a2﹣a1=a3﹣a2,即(4t2﹣3t2+2t)﹣1=(6t2﹣3t2+2t)﹣(4t2﹣3t2+2t)
所以t=1,即an=2n﹣1。
(3)由于an=a1+(n﹣1)d,

即数列{bn}是公比大于0,首项大于0的等比数列,记其公比是q(q>0)。
以下证明:b1+bn≥bp+bk,其中p,k为正整数,且p+k=1+n。
∵(b1+bn)﹣(bp+bk)=

当q>1时,因为y=qx为增函数,p﹣1≥0,k﹣1≥0,
∴qp﹣1﹣1≥0,qk﹣1﹣1≥0,∴b1+bn≥bp+bk;
当q=1时,b1+bn=bp+bk;
当q=1时,因为y=qx为减函数,p﹣1≥0,k﹣1≥0,
∴qp﹣1﹣1≤0,qk﹣1﹣1≤0,∴b1+bn≥bp+bk,
综上:b1+bn≥bp+bk,其中p,k为正整数,且p+k=1+n。
∴n(b1+bn)=(b1+bn)+(b1+bn)+…(b1+bn)≥(b1+bn)+(b2+bn﹣1)+…(bn+b1)
=(b1+b2+…+bn)+(bn+bn﹣1+…+b1),
即
知识点
已知等比数列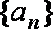
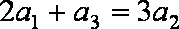
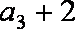
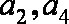
(1)求数列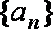
(2)若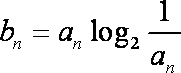
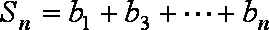
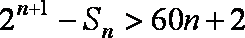
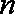
正确答案
(1)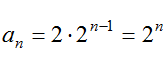
解析
解析:(1)设等比数列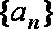
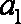
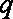
依题意,有
由①及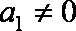
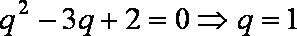
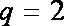
当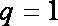
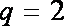
把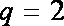
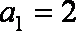
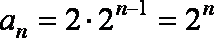
(2)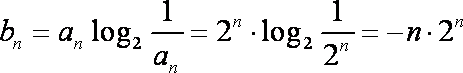
∴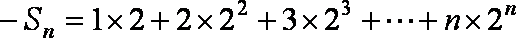
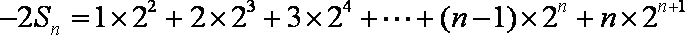
③-④得
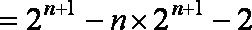
由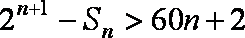
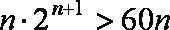
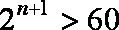
又当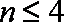
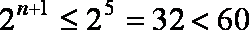
当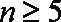
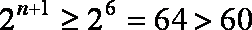
故使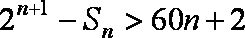
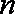
知识点
设实数


正确答案
解析
由于实数








知识点
已知数列




(1)求数列
(2)若对一切

正确答案
(1)
解析
解析:(1)由题意可知当
当


用①式减去②式得:
所以数列

(2)因为
当对一切

①当


②当 


综合以上可知
知识点
扫码查看完整答案与解析