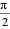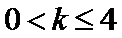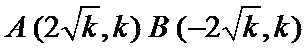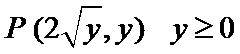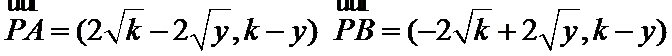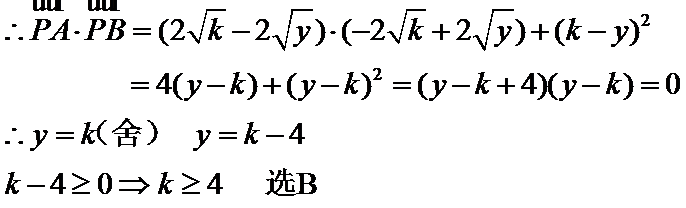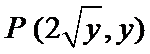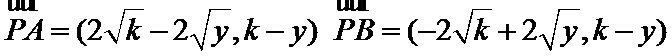- 量积判断两个平面向量的垂直关系
- 共78题
1
题型:
单选题
|
4.设

正确答案
D
知识点
数量积的坐标表达式数量积表示两个向量的夹角量积判断两个平面向量的垂直关系
1
题型:简答题
|
已知角







正确答案
解:(1)由

且

∴

∴
(2)由余弦定理得
,而∵
由


当且仅当
又


所以

解析
本题属于三角函数的基本问题,题目的难度是中等,本题的关键是:
(1)、向量的基本运算以及三角函数恒等变换的应用;
(2)、余弦定理与基本不等式之间的应用,一直是考试的热点问题,
考查方向
本题考查了向量运算、三角函数恒等变换、正弦定理和余弦定理的综合应用
易错点
向量的运算、余弦定理的应用,需要注意
知识点
三角函数中的恒等变换应用余弦定理平面向量数量积的运算量积判断两个平面向量的垂直关系
1
题型:简答题
|
13.向量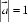
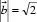
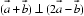

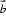
正确答案
解析
由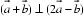
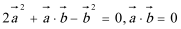

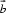
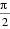
考查方向
本题主要考查了平面向量的夹角公式。
解题思路
本题考查平面向量的夹角公式,解题步骤如下:
1、利用垂直条件求出数量积。
2、利用夹角公式求解.
易错点
本题必须注意数量积的公式。
知识点
向量的模数量积表示两个向量的夹角量积判断两个平面向量的垂直关系
1
题型:简答题
|
13.已知平面直角坐标系中,



正确答案
解析
向量a在向量b的方向上的投影是,
考查方向
向量的数量积的概念.
解题思路
利用向量的数量积性质求解
易错点
向量的在另一个向量上投影的概念理解有误
知识点
平面向量数量积的运算量积判断两个平面向量的垂直关系
1
题型:
单选题
|
10.已知抛物线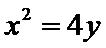
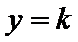
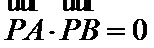
正确答案
B
解析
抛物线与直线y=k联立确定AB两点的坐标
设动点
则
考查方向
本题主要考察了抛物线的定义及其标准方程,考察了抛物线的几何意义,考察了向量的数量积运算,考察了向量的坐标运算,考察了存在性问题求解,该题多知识点交汇,题目较难,解题多注意细节
解题思路
本题属于多知识迁移题,需要对知识进行有效转换
(1)确定AB两点的坐标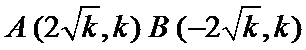
(2)向量
(3)利用向量的数量积运算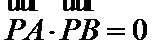
易错点
该题主要易错于题意理解错误,不能有效进行知识的转换
知识点
量积判断两个平面向量的垂直关系抛物线的标准方程和几何性质
下一知识点 : 平面向量数量积坐标表示的应用
扫码查看完整答案与解析