- 平行公理
- 共49题
已知椭圆C:





(1) 求椭圆方程
(2)过椭圆的左顶点A作两条弦







正确答案
(1) 

解析
(1)由

(2)椭圆方程: 即
当直线AM的斜率变化时,设AM的斜率为k,则AN的斜率为
直线AM方程:y=k(x+2)
直线AN方程:y= 
将AM方程代入椭圆,整理:
韦达定理:



将AN方程代入椭圆,整理:
韦达定理:



直线MN的斜率

直线MN方程:y


化简:y= 

由此,可知,过定点(
知识点
如图,某测量人员,为了测量西江北岸不能到达的两点A,B之间的距离,她在西江南岸找到一个点C,从C点可以观察到点A,B;找到一个点D,从D点可以观察到点A,C;到一个点E,从E点可以观察到点B,C;并测量得到数据:∠ACD=90°,∠ADC= 60°,∠ACB =15°,∠BCE =105°,∠CEB =45°,DC=CE =1(百米)。
(1)求△CDE的面积;
(2)求A,B之间的距离。
正确答案
(1)

解析
(1)连结DE,在CDE中,

(2)依题意知,在RTACD中,
在BCE中,
由正弦定理
得
∵

在ABC中,由余弦定理
可得
∴
知识点
有如下四个命题:
①若直线l1:2kx+(k+1)y+1=0与直线l2:x﹣ky+2=0垂直,则实数k=1;
②若函数f(x)=sin(ωx+

③已知定义在R上的偶函数f(x)满足f(2+x)=f(2﹣x),且f(1)=1则f(2011)=1
④曲线C:

其中正确命题的序号为 _________ 。
正确答案
②③
解析
①若直线l1:2kx+(k+1)y+1=0与直线l2:x﹣ky+2=0垂直,则实数k=1;而k=0时两条直线垂直,所以不正确。
②若函数f(x)=sin(ωx+





③已知定义在R上的偶函数f(x)满足f(2+x)=f(2﹣x),函数的周期为4且f(1)=1则f(2011)=f(3)=f(1)=1,正确;
④曲线C:

故答案为:②③
知识点
若函数


正确答案
解析
函数




知识点
在△ABC中,角A,B,C的对边分别为a,b,c,已知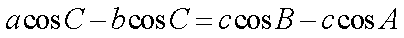
且C=120°。
(1)求角A;
(2)若a=2,求c。
正确答案
见解析
解析
(1)由正弦定理,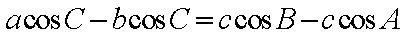
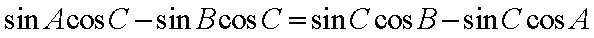
所以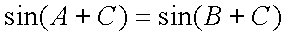
因为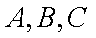
所以
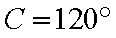
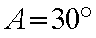
(2)由(1)知,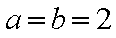
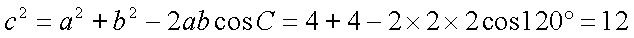
所以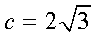
知识点
某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160 cm和184 cm之间,将测量结果按如下方式分成6组:第一组 [160,164],第二组[164,168],…,第6组[180,184],下图是按上述分组方法得到的频率分布直方图。
(1)试评估该校高三年级男生在全市高中男生中的平均身高状况;
(2)求这50名男生身高在172 cm以上(含172 cm)的人数;
(3)在这50名男生身高在172 cm以上(含172 cm)的人中任意抽取2人,该2人中身高排名(从高到低)在全市前130名的人数记为

参考数据:若



正确答案
见解析
解析
(1)由直方图,经过计算该校高三年级男生平均身高为

高于全市的平均值168(或者:经过计算该校高三年级男生平均身高为168.72,比较接近全市的平均值168).
(2)由频率分布直方图知,后三组频率为(0.02+0.02+0.01)×4=0.2,人数为0.2×5=10,即这50名男生身高在172 cm以上(含172 cm)的人数为10人.
(3)

所以,全市前130名的身高在180 cm以上,这50人中180 cm以上的有2人.
随机变量




知识点
从某学校高三年级共1000名男生中随机抽取50人测量身高。据测量,被测学生身高全部介于155cm到195cm之间,将测量结果按如下方式分成八组,第一组[155,160),第二组[160,165),… ,第八组[190,195]。下图是按上述分组方法得到的频率分布直方图的一部分、其中第六组、第七组、第八组人数依次构成等差数列。
(1)求第六组、第七组的频率,并估算高三年级全体男生身高在180cm以上(含180cm)的人数;
(2)学校决定让这50人在运动会上组成一个高旗队,在这50人中要选身高在180cm以上(含180cm)的三人作为队长,记X为身高在[180,185)的人数,求X的分布列和数学期望。
正确答案
见解析
解析
解: (1) 第六组
第七组
估计人数为
(2)


所以


知识点
已知各项全不为零的数列






正确答案
解析
①-②可得:
知识点
18.如图,在四棱锥







(Ⅰ)求证:

(Ⅱ)设点





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.阅读下面题目柯西不等式的解法,再根据要求解决后面的问题.
阅读题目:对于任意实数
.
证明:构造函数

注意到

即


问题:
(1)请用柯西不等式的结论证明:对任意正实数

(2)对任意正实数



(3)根据阅读题目的证明,将不等式
正确答案
(1)因为都是
所以不等式
(其中等号成立当且仅当,即
(2)因为0<
(其中等号成立当且仅当

所以函数

(3)可将不等式推广到

不等式
成立
证明如下:
设
注意到
即
其中等号成立当且仅当
即
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析







































