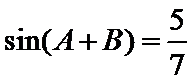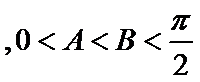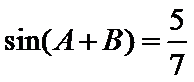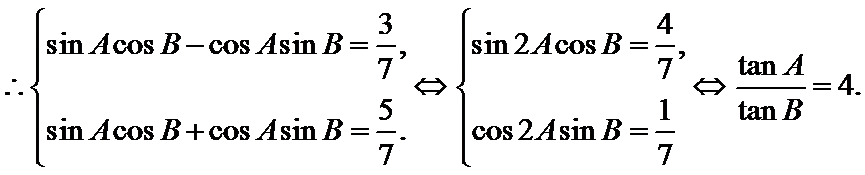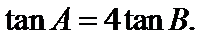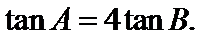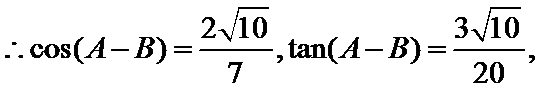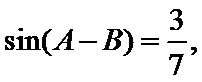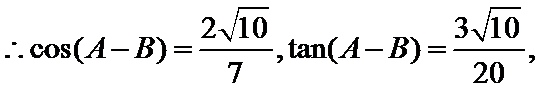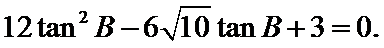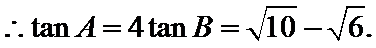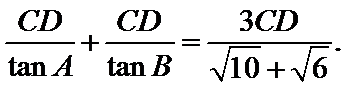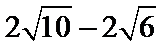- 导数的运算
- 共219题
1
题型:
单选题
|
12.已知函数


正确答案
B
解析
由函数











考查方向
本题主要考查了函数的零点、导数在研究函数的性质中的应用等知识同时考查了转化与化归的数学思想方法。
解题思路
先要根据两个函数的图像上存在关于x轴对称的点这一信息建立关于a的关系,再利用导数求解。
易错点
本题容易因为不能准确判断两函数的图像存在关于x轴对称的点这一信息而导致不会做。
知识点
导数的运算
1
题型:
单选题
|
12.已知函数




正确答案
D
解析
因为










考查方向
积分与求导;函数的性质;函数的最大值
解题思路
先根据所给条件变形并积分,得到f(x),进而求出函数的最大值最小值
易错点
计算失误,积分与求导关系弄混淆
知识点
导数的运算
1
题型:简答题
|
已知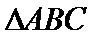
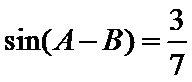
17.求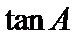
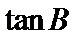
18.若AB=6,求AB边上的高CD
第(1)小题正确答案及相关解析
正确答案
(Ⅰ)证明: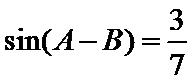
所以
解析
(Ⅰ)证明: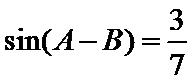
所以
考查方向
本题主要考察了两角和差的应用,考察了三角恒等变换的应用,解三角型的应用,三角函数中的几何运算
解题思路
该题解题思路如下
1)利用两角和差公式 对解析式化简
2)由已知可得到角的范围
易错点
该题对于三角形中的角的关系出错,和角公式展开化简计算错误
第(2)小题正确答案及相关解析
正确答案
(II)解: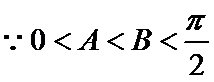
即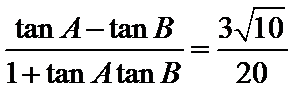
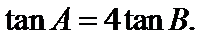
解得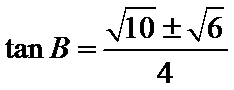
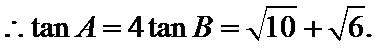
设AB边上的高为CD.
则AB=AD+DB=
或AB=AD+DB=
由AB=6,得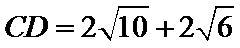
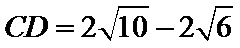
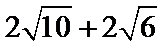
解析
(II)解: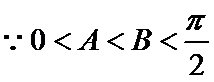
即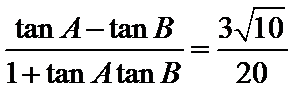
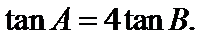
解得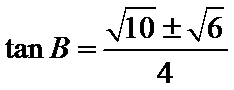
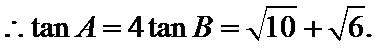
设AB边上的高为CD.
则AB=AD+DB=
或AB=AD+DB=
由AB=6,得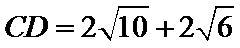
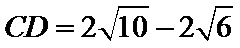
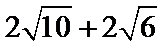
考查方向
本题主要考察解三角型的应用,三角函数中的几何运算
解题思路
该题解题思路如下
对解析式解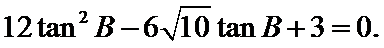
易错点
该题对于三角形中的角与边的关系出错
1
题型:
单选题
|
正确答案
A
知识点
函数奇偶性的性质导数的运算其它不等式的解法
1
题型:简答题
|
正确答案
知识点
函数单调性的判断与证明导数的运算不等式恒成立问题
下一知识点 : 导数的加法与减法法则
扫码查看完整答案与解析