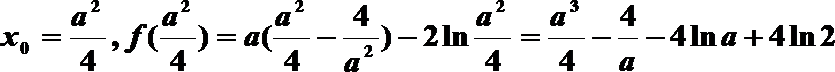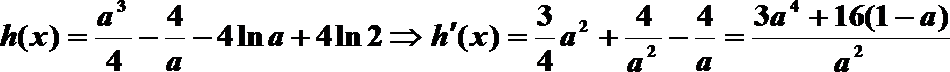- 导数的运算
- 共219题
10.已知函数f(x)=x+




f(x1)≥g(x2),则实数a的取值范围是
正确答案
解析
f(x)min=f(1)=5, g(x)min = g(2)=4+a,得a≤1。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查函数的值域
解题思路
1、求出f(x)在[
2、求出f(x)min≥g(x)min,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断范围大小时发生错误。
知识点
21. 设函数f(x)=

(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当m≥0时,讨论函数f(x)与g(x)图象的交点个数.
正确答案
(1)当






解析
⑴解:函数


当



当

当


当


综上:当














































考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
1、求导,然后解导数不等式,求单调区间。
2、对参数分类讨论得结论。
易错点
第二问中的易丢对a的分类讨论。
知识点
10.若


正确答案
解析
函数在R上有两个相异的极值点等价于它的导函数有两个不等的实数根,即根的判别式为大于零,可以得到

考查方向
本题主要考查概率的集合概型,导数的运用,属于难题。
解题思路
先求导,利用根的判别式判断,最后利用几何概型求解。
易错点
不理解,不会将未知内容转化成已学过的知识。
知识点
21. 已知函数
(I)若
(II)若


(III)设b=0,若存在

正确答案
解:(Ⅰ) 

定义域为
在


当
所以,函数

(Ⅱ)因为


(i) 若




故函数

此时
(ii)若

当

当


当


故
(Ⅲ) 
不等式
可化为
因为

所以



令


当


从而



故


解析
将f(x)求导并整理,得到f(x)在区间上单调递减,然后分类讨论a的不同取值对单调区间的影响。利用函数单调性证明不等式恒成立的条件。解题步骤见答案。
考查方向
本题主要考查函数的单调性、奇偶性,导数的应用,参数的分类讨论等,常和不等式方程相结合考查,属于难题。
解题思路
利用导数求单调区间,利用函数与不等式关系求最大值最小值
易错点
不会利用导数求函数单调区间
知识点
12.关于函数
正确答案
解析


且当

当

因此



所以当


又

所以
设
易知当

对任意的正实数
显然当



所以
作为选择题这时可得结论,选C,
下面对D研究,因为
即

设




又
所以

考查方向
函数的性质,知识点多,难度大。
解题思路
根据函数的性质,依次判断每个选项
易错点
对命题理解不透彻,对函数的性质掌握不好
知识点
21.已知函数




(Ⅰ)若


(Ⅱ)若


正确答案
见解析
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)要注意对参数的讨论.
(Ⅰ)由











(Ⅱ)由


所以

因此,对任意


由



因此,当








设





故


所以
因此,对任意

考查方向
本题考查了利用导数求参数的取值范围,分类讨论,讨论点大体可以分成以下几类:1、根据判别式讨论;2、根据二次函数的根的大小;3、定义域由限制时,根据定义域的隐含条件;4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;5、多次求导求解等.
解题思路
本题考查导数的性质,解题步骤如下:
1、求导,然后解导数不等式。
2、对参数分类讨论证得结论。
易错点
第二问中的易丢对x的分类讨论。
知识点
21.己知函数f(x)=a(x-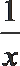
(1)若f(x)有极值,求a的取值范围;
(2)讨论(x)的零点个数,并说明理由.(参考数值:ln2≈0. 6931)
正确答案
(1)0<a<1;
(2)当a≤0或a≥1时,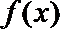
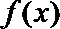
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)要注意对参数的讨论.
(1)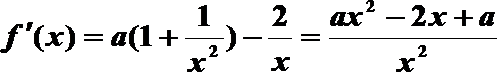
所以ax2-2x+a=0有正根且不为等根。显然a≠0,由x1x2=1>0.得Δ>0且x1+x2>0,
所以 0<a<1 。
(2)由上知,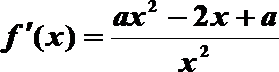
①若a≤0,则
因为f(1)=0,所以f(x)的零点唯一;
②若a≥1,则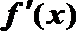
因为f(1)=0,所以f(x)的零点唯一;
③若0<a<1,记x1,x2分别为ax2-2x+a=0的两根,且x1<1<x2,且f(x)在(0,x1)单调递增,在(x1,x2)单调递增,(x2,+∞)单调递增。
因为f(1)=0,所以f(x1)>0,f(x2)<0.
当x∈(0,x1)时,取
令
显然,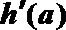
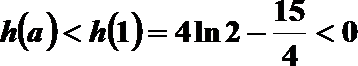
故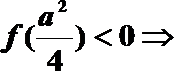
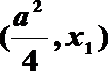
因为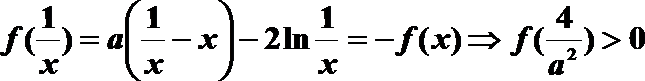
则f(x)在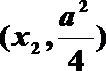
综上可知:当a≤0或a≥1时,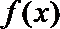
当0<a<1时,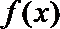
考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
(1)根据判别式讨论;
(2)根据二次函数的根的大小;
(3)定义域由限制时,根据定义域的隐含条件;
(4)求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
(5)多次求导求解等.
解题思路
本题考查导数的性质,解题步骤如下:
(1)求导,然后解导数不等式,算极值。
(2)对参数分类讨论求得零点个数。
易错点
第二问中的易丢对a的分类讨论。
知识点
12. 已知函数


正确答案
解析
构造函数


因为 



所以
故选A。
考查方向
本题主要考查构造函数比较两个数大小的方法,导数与函数的单调性等知识,是一道综合性较强的问题。
解题思路
(1)根据题意构造函数。
(2)确定函数的单调性。
(3)利用单调性比较大小。
易错点
(1)不能根据题意构造函数。
(2)求函数导数时,出现错误。
知识点
20.已知函数

(Ⅰ)求函数
(Ⅱ)求证:对于任意


(Ⅲ)试确定曲线

正确答案
(Ⅰ)所以函数

(Ⅲ)当





解析
(Ⅰ)解:函数

求导,得
令

当


所以函数



所以函数

(Ⅱ)证明:假设存在某个


设切点为

所以切线满足斜率

所以
即
所以假设不成立.
所以对于任意


(Ⅲ)解:“曲线


由方程

令



考察函数

因为
所以函数


而方程


所以当



故当





考查方向
解题思路
1、第一问写出函数的定义域,求出导数,然后令导数等于零解方程,列表求极值。
2、第二问直接不易证明,可考虑使用反证法:假设存在某个


3、判断曲线与直线的交点个数问题可以考虑通过函数的极值与直线的相对位置关系以及函数图像的特点采用数形结合的方法判断交点个数;也可以转化为方程判断根的个数进而确定图像交点的个数。由第一问可看出


易错点
第一问中不交待极大值不存在而失分或未考虑函数的定义域而出错;
知识点
21. 设函数

(1)当

(2)若



求证:

正确答案
(1)函数单调增区间为:



(2)略.
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,
(1)直接按照步骤来求;(2)要注意对参数的讨论.
(Ⅰ)函数



令:


所以函数单调增区间为:


所以函数单调减区间为:
(Ⅱ)证明:
令:
所以:



不妨设

由


由

所以




当

当
所以:

设:

所以:
又:
所以:
考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
本题考查导数的性质,解题步骤如下:
1、求导,然后解导数不等式,求单调区间。
2、对参数分类讨论证得结论。
易错点
第二问中的易丢对a的分类讨论。
知识点
扫码查看完整答案与解析