- 导数的运算
- 共219题
20.(本小题满分13分)
已知
(I)讨论
(II)当


正确答案
知识点
21.(本小题满分12分)
(I)讨论函数

(II)证明:当



正确答案
知识点
22.已知函数



(1)求函数
(2)若


正确答案
(1)①当



②当


(2)
解析
(1)
①当



②当


(2)由题意得
构造函数
显然




当





当











考查方向
本题主要考查利用导数求函数的单调区间及解决不等式中的恒成立问题,综合性较强。
解题思路
(1)求出导数,再分类讨论求单调区间。
(2)构造函数把恒成立问题转化为求最值问题。
易错点
(1)第一问不能对b进行分类讨论。
(2)第二问不能转化为恒成立问题解决。
(3)分类讨论不严密。
知识点
21
(1)求f(x)的单调区间,
(2)若k∈Z,且f(x-1)+x>k (1-3 )对任意x>1恒成立,求k的最大值,
(3)对于在区间(0,1)上的任意一个常数a,是否存在正数x。,使得ef(x0 ) < 1 -

正确答案
(1)f(x)的单调递增区间是
(2)4;
(3)存在正数x。
解析
考查方向
本题考查了利用导数求单调区间,导数与不等式综合应用求恒成立问题和存在性问题
解题思路
易错点
1、第二问中的易丢对K的分类讨论。
知识点
16.已知

的零点个数为___________.
正确答案
0
解析
考查方向
解题思路
易错点
无法从条件中捕捉到有效信息,向结论靠拢。
知识点
(本小题满分13分)
已知函数
(Ⅰ)求函数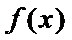
(Ⅱ)当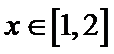
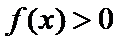
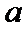
(Ⅲ)试问过点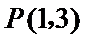
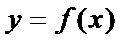
正确答案
考查方向
易错点
1、第一问在对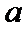
知识点
16.f(x)是定义在R上的函数,其导函数为f'(x),若f(x)—f'(x) <1,f(0) = 2016,则不等式e x f(x) >e x + 2015(其中e为自然对数的底数)的解集为 .
正确答案
解析
设



考查方向
本题主要考查导数与不等式综合应用
解题思路
构造函数

易错点
如何构造函数,利用函数的单调性求解
知识点
21.已知函数




(Ⅰ)求

(Ⅱ)证明:当

(Ⅲ)证明:对任意给定的正数



正确答案
(Ⅰ)见解析
(Ⅱ)见解析
(Ⅲ)见解析
解析
(Ⅰ)解,由

因为

所以

令

当



所以当


(Ⅱ)证明,令

由(Ⅰ)得

所以当


(Ⅲ)证明一,①若

由(Ⅱ)知,当



取


②若

要使不等式

而要使


令

所以当


取


又
易知
所以



综上,对任意给定的正数



证明二,对任意给定的正数

由(Ⅱ)知,当


当

因此,对任意给定的正数



证明三,首先证明当

令

由(Ⅱ)知,当

从而


所以

取


因此,对任意给定的正数



考查方向
解题思路
易错点
第一问建议做出极值表便于观察,防止出错;
第二问忽略证明第一问时得到的结论。
知识点
10.已知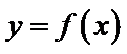
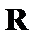
且当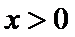
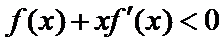
若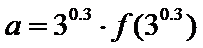
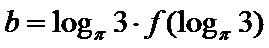
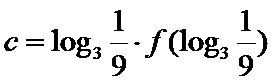
则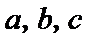
正确答案
解析
试题分析:令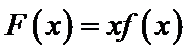
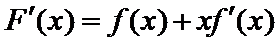
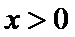
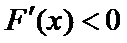
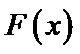
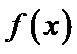
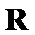
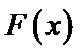
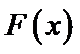
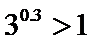
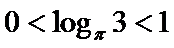
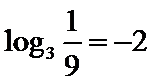
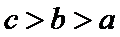
考查方向
解题思路
构造函数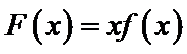
易错点
不能构造出新函数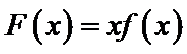
知识点
21.已知函数
(1)若

(2)证明:
正确答案
(1)
(2)见解析.
解析
试题分析:本题属于导数与函数最值的关系、不等式恒成立问题等知识点的综合应用问题,属于拔高题,第二问不容易得分,解析如下:
(1)解:由

即:


在(0,1)上,


所以h(x)在x=1时,取得最大值h(1)=1,即
(2)证明:由(1)知,当k=1时,
令

所以有:


累加得:
考查方向
解题思路
由函数的极值、最值逆求参数的值(或取值范围)问题,往往需要对参数进行分类讨论,如何划分参数讨论的区间成为思维的难点.由于这类问题涉及函数的单调区间,因此分类的标准是使函数在指定的区间内其导数
易错点
相关知识点不熟容易证错。
知识点
扫码查看完整答案与解析