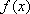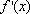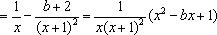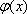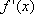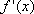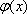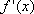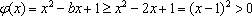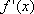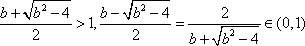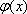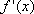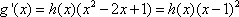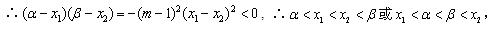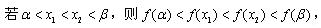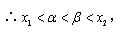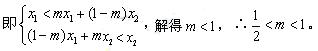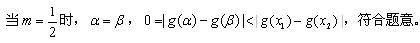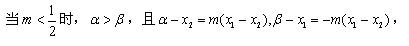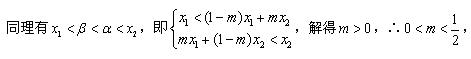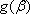- 导数的运算
- 共219题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
设L为曲线C:
(1)求L的方程;
(2)证明:除切点(1,0)之外,曲线C在直线L的下方。
正确答案
见解析
解析
(1)设

所以f′(1)=1.
所以L的方程为y=x-1.
(2)令g(x)=x-1-f(x),则除切点之外,曲线C在直线L的下方等价于g(x)>0(
g(x)满足g(1)=0,且g′(x)=1-f′(x)=
当0<x<1时,x2-1<0,ln x<0,所以g′(x)<0,故g(x)单调递减;
当x>1时,x2-1>0,ln x>0,所以g′(x)>0,故g(x)单调递增。
所以,g(x)>g(1)=0(
所以除切点之外,曲线C在直线L的下方。
知识点
设函数fn(x)=
(1)对每个n∈N*,存在唯一的xn∈
(2)对任意p∈N*,由(1)中xn构成的数列{xn}满足0<xn-xn+p<.
正确答案
见解析
解析
(1)对每个n∈N*,当x>0时,f′n(x)=
由于f1(1)=0,当n≥2时,fn(1)=
又

所以存在唯一的xn∈
(2)当x>0时,fn+1(x)=fn(x)+
由fn+1(x)在(0,+∞)内单调递增知,xn+1<xn,故{xn}为单调递减数列,
从而对任意n,p∈N*,xn+p<xn.
对任意p∈N*,
由于fn(xn)=
fn+p(xn+p)=
①式减去②式并移项,利用0<xn+p<xn≤1,
得xn-xn+p=

因此,对任意p∈N*,都有0<xn-xn+p<
知识点
设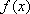
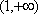
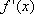

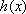

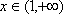
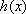
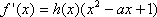
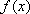
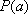
(1)设函数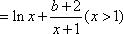

(i)求证:函数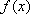
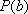
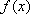
(2)已知函数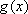
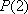
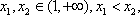
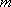
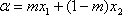
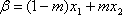

若|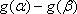
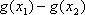
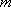
正确答案
见解析。
解析
(1)(i)
∵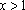
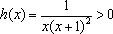
∴函数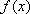
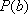
(ii)(方法一)设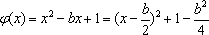
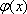
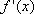
当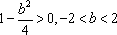
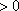
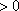
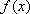
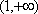
当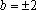
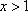
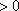
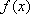
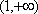
当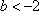
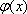

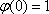
对于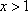
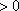
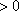
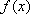
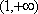
(方法二)当
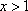
所以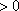
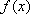
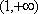
当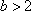
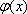
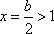
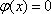
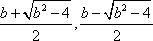
当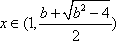
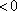
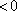
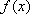
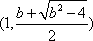
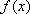

综上所述,当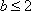
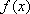
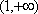
当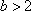
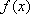
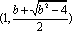
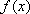
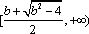
(2)(方法一)由题意,得:
又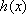
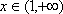

所以对任意的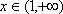
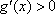
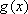
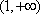
又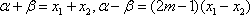
当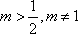
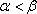
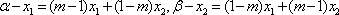
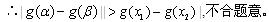
综合以上讨论,得:所求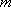
(方法二)由题设知,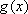
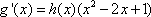
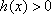
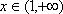
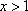
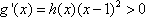
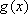
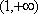
①当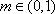
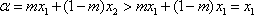
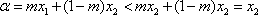
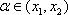
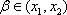
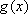
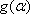
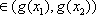
从而有|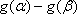
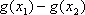
②当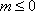
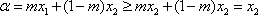
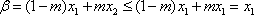
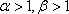
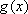
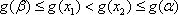
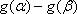
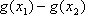
③当
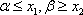
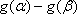
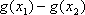
因此综合①、②、③得所求的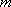
知识点
已知函数

(1)若对一切


(2)在函数






正确答案
见解析
解析
(1)若



故
而
当





于是对一切

令
当



故当




综上所述,

(2)由题意知,
令
令

当



故当

从而

所以
因为函数








综上所述,存在



知识点
扫码查看完整答案与解析