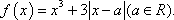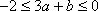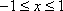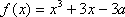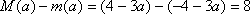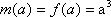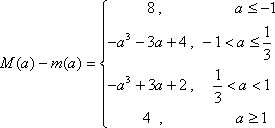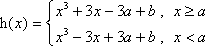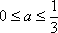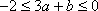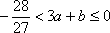- 导数的运算
- 共219题
设a+b=2,b>0,则当a=__________时,
正确答案
-2
解析
因为a+b=2,所以
1=
≥
当a>0时,

当a<0时,

因为b>0,所以原式取最小值时b=-2a.
又a+b=2,所以a=-2时,原式取得最小值。
知识点
已知函数

正确答案
解析
由






知识点
设函数






正确答案
解析
由
故
由
故
=
故
知识点
已知函数f(x)=x2ln x.
(1)求函数f(x)的单调区间;
(2)证明:对任意的t>0,存在唯一的s,使t=f(s);
(3)设(2)中所确定的s关于t的函数为s=g(t),证明:当t>e2时,有
正确答案
见解析
解析
(1)函数f(x)的定义域为(0,+∞)。
f′(x)=2xln x+x=x(2ln x+1),令f′(x)=0,得
当x变化时,f′(x),f(x)的变化情况如下表:
所以函数f(x)的单调递减区间是

(2)证明:当0<x≤1时,f(x)≤0.
设t>0,令h(x)=f(x)-t,x∈[1,+∞)。
由(1)知,h(x)在区间(1,+∞)内单调递增。
h(1)=-t<0,h(et)=e2tln et-t=t(e2t-1)>0.
故存在唯一的s∈(1,+∞),使得t=f(s)成立。
(3)证明:因为s=g(t),由(2)知,t=f(s),且s>1,从而

其中u=ln s.
要使

当t>e2时,若s=g(t)≤e,则由f(s)的单调性,有t=f(s)≤f(e)=e2,矛盾。
所以s>e,即u>1,从而ln u>0成立。
另一方面,令F(u)=

当1<u<2时,F′(u)>0;当u>2时,F′(u)<0.
故对u>1,F(u)≤F(2)<0.
因此
综上,当t>e2时,有
知识点
已知函数
(1) 若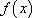
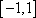
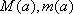
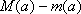
(2) 设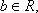
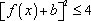
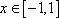
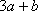
正确答案
(1)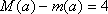
解析
(1)∵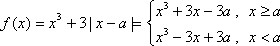
∴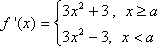
(ⅰ)当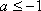
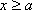
此时,f(x)在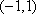
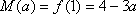
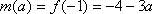
故
(ⅱ)当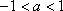
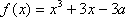
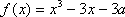
∴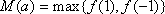
由于
当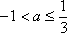
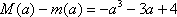
当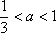
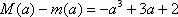
(ⅲ)当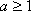

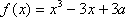
此时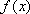
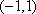
因此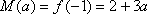
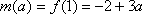
故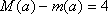
综上,
(2)令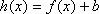
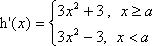
因为[f(x)+b]2≤4对x∈[-1,1]恒成立,
即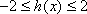
所以由(1)知,
(ⅰ)当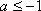
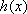
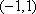
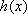
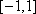
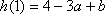
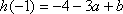
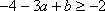
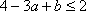
(ⅱ)当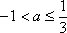

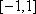
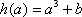
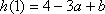
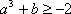
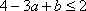
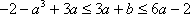
令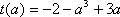

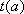
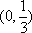
故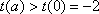
因此
(ⅲ)当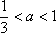
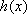

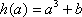
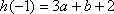
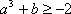
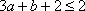
(ⅳ)当


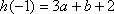
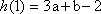
所以由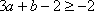
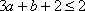
综上,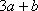
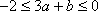
知识点
扫码查看完整答案与解析