导数的运算
共219题

· 导数的运算

导数的运算
共219题

热门试卷

X 查看更多试卷

题型：简答题

简答题 · 15 分

已知，函数

（1）求曲线在点处的切线方程；

（2）当时，求的最大值。

正确答案

（1）（2）

解析

（1）由已知得：，且，所以所求切线方程为：，即为：；

（2）由已知得到：，其中，当时，，

（1）当时，，所以在上递减，所以，因为；

（2）当，即时，恒成立，所以在上递增，所以，因为

；

（3）当，即时，

，且，即

所以，且

所以，

所以；

由，所以

（ⅰ）当时，，所以时，递增，时，递减，所以，因为

，又因为，所以，所以，所以

（ⅱ）当时，，所以，因为，此时，当时，是大于零还是小于零不确定，所以

1当时，，所以，所以此时；

2当时，，所以，所以此时

综上所述：

知识点

函数的值域导数的几何意义导数的运算

题型：简答题

简答题 · 14 分

已知a是给定的实常数，

设函数是的一个极大值点.

（1）求b的取值范围;

（2）设是的3个极值点，问是否存在实数b，可找到，使得的某种排列（其中）依次成等差数列？若存在，示所有的b及相应的若不存在，说明理由.

正确答案

见解析

解析

（1）解：

令

则

于是可设是的两实根，且

1）当时，则不是的极值点，此时不合题意

2）当时，由于是的极大值点，

故即

即

所以

所以的取值范围是（-∞，）

（2）解：由（Ⅰ）可知，假设存了及满足题意，则

1）当时，则

于是

即

此时

或

2）当时，则

①若

于是

即

于是

此时

②若

于是

即

于是

此时

综上所述，存在满足题意

当

知识点

导数的几何意义导数的运算等差数列的性质及应用

题型：单选题

单选题 · 5 分

已知为R上的可导函数，且均有，则有（）

正确答案

解析

略。

知识点

导数的运算

题型：单选题

单选题 · 5 分

已知为自然对数的底数，设函数，则

A当时，在处取得极小值

B当时，在处取得极大值

C当时，在处取得极小值

D当时，在处取得极大值

正确答案

解析

当时，，且，所以当时，，函数递增；当时，，函数递减；所以当时函数取得极小值；所以选C

知识点

导数的几何意义导数的运算

题型：简答题

简答题 · 12 分

21．已知函数.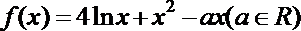

（1）当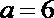时,求函数的单调区间;

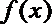
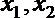
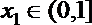
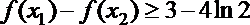
（2）若函数有两个极值点,且,求证:;

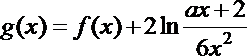
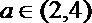
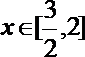
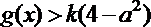
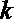
（3）设,对于任意时,总存在,使成立，求实数的取值范围.

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的运算

继续学习学习下一知识点

下一知识点 : 导数的加法与减法法则

百度题库 > 高考 > 理科数学 > 导数的运算

扫码查看完整答案与解析