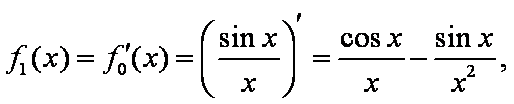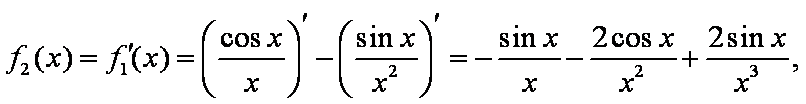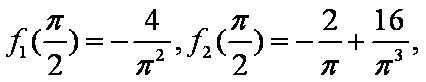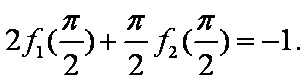- 导数的运算
- 共219题
已知矩阵





正确答案
见解析。
解析




知识点
某工厂生产某种产品,每日的成本C(单位:万元)与日产量x(单
位:吨)满足函数关系式C=3+x,每日的销售额S(单位:万元)与日产量x的函数关
系式
(1)求k的值;
(2)当日产量为多少吨时,每日的利润达到最大,并求出最大值。
正确答案
(1)18(2)5吨;6万元
解析
解析:(1)依题意得当x=2时L=3
(2)①当0<x<6时
②当x≥6时,显然有L≤5(当且仅当x=6时取“=”号)
综上知:当日产量为5吨时,每日的利润达到最大,最大值为6万元。
知识点
已知





(1)求
(2)求函数
正确答案
(1)
解析
(1)设


则由

可得

(2)


所以,当


知识点
已知函数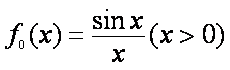
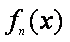
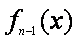
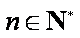
(1)求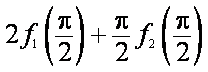
(2)证明:对任意的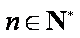
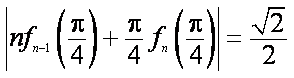
正确答案
见解析。
解析
(1)由已知,得
于是
所以
故
(2)证明:由已知,得
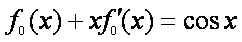
即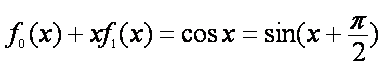
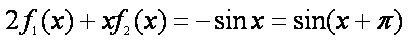
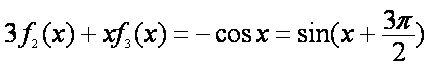
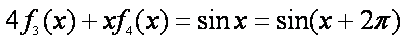
下面用数学归纳法证明等式
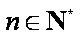
(i)当n=1时,由上可知等式成立.
(ii)假设当n=k时等式成立, 即
因为
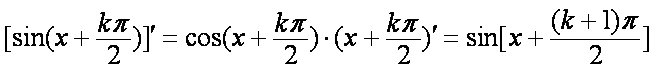
所以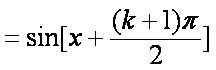
所以当n=k+1时,等式也成立.
综合(i),(ii)可知等式
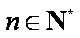
令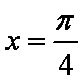
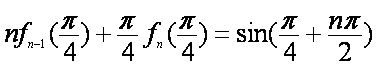
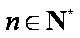
所以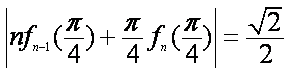
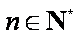
知识点
如图所示, 四棱锥P-ABCD的底面是边长为1的正方形,PACD,PA = 1, PD=,E为PD上一点,PE = 2ED。
(1)求证:PA 
(2)求二面角D-AC-E的余弦值;
(3)在侧棱PC上是否存在一点F,使得BF // 平面AEC?若存在,指出F点的位置,并证明;若不存在,说明理由。
正确答案
见解析
解析
(1) 


又PA 


(2)过E作EG//PA 交AD于G,从而EG 
且AG = 2GD , EG = PA =
连接BD交AC于O, 过G作GH//OD ,交AC于H,
连接EH。










(3)以AB , AD , PA为x轴、y轴、z轴建立空间直角坐标系。
则A(0 ,0, 0),B(1,0,0) ,C(1,1,0),P(0,0,1),E(0 ,



设平面AEC的法向量


则
假设侧棱PC上存在一点F, 且

(


又因为:














所以存在PC的中点F, 使得BF//平面AEC。 ----------------12分
20解析:(1)由f/(x)=


(2)当a=1时,f(x)= ln(1+x)—x. (x>-1)
f/(x)=
由f/(x)=0
当x∈(0,+∞)时,f/(x)<0,此时f(x)递减
即f(x)在(-1,0)上单调增,在(0,+∞)上单调减…………………………8分
(3)由(2)知f(x)≤f(0)=0在(-1,+∞)内恒成立
∴ln (1+x) ≤x
∴ex≥1+x 
∴≤
即h(x)=(ex-P)2+(P-x)2≥
知识点
扫码查看完整答案与解析