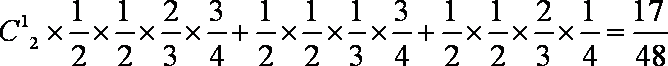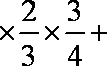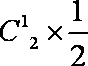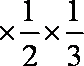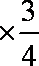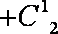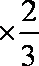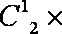- 随机事件及其概率
- 共504题
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前


(1)求该校报考飞行员的总人数;
(2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设X表示体重超过60公斤的学生人数,求X的分布列和数学期望。
正确答案
见解析。
解析
(1)设报考飞行员的人数为


又因为
(2) 由(1)可得,一个报考学生体重超过60公斤的概率为

所以


则

知识点
2012年伦敦奥运会某项目参赛领导小组要从甲、乙、丙、丁、戊五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中甲、乙只能从事前三项工作,其余三人均能从事这四项工作,则不同的选派方案共有
正确答案
解析
分两类:第一类,甲、乙两人只选一人参加,共有:
第二类:甲、乙两人都选上,共有:
知识点
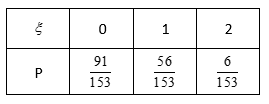
天津高考数学试卷共有8道选择题,在每小题给出的四个选项中,只有一项是符合题目要求的,评分标准规定:“选对得5分,不选或选错得0分”,某考生已确定有4道题答案是正确的,其余题中:有两道只能分别判断2个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜,求:
(1)该考生得40分的概率;
(2)写出该考生所得分数孝的分布列,并求:
①该考生得多少分的可能性最大?
②该考生所得分数ξ的数学期望•
正确答案
见解析。
解析
(1)设选对一道“可判断2个选项是错误的”题目为事件A,
“可判断1个选项是错误的”该题选对为事件B,
“不能理解题意的”该题选对为事件C,
则P(A)=


∴该考生得40分的概率:
P=[P(A)]2•P(B)•P(C)=

(2)①该考生所得分数ξ=20,25,30,35,40,
P(ξ=20)=[P(




P(ξ=25)=

=


P(ξ=30)=
=


P(ξ=35)=
=


P(ξ=40)=1﹣
∴该考生得25分或30分的可能性最大。
②Eξ=20×

知识点
某班同学利用国庆节进行社会实践,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”否则称为“非低碳族”,得到如右统计表,但由于不小心表中字母表示的部分数据丢失,现知道被调查的人中低碳族占65%,则40岁及其以上人群中,低碳族占该部分人数的频率为 。
正确答案
0.6
解析
由题意,n=
∵被调查的人中低碳族占65%,
∴被调查的人中低碳族有650人,
∴40岁及其以上低碳族有650﹣120﹣196﹣100=234人,
∵40岁及其以上共有1000﹣200﹣300﹣110=390人,
∴40岁及其以上人群中,低碳族占该部分人数的频率为
知识点
某校从高二年级4个班中选出18名学生参加全国数学联赛,学生来源人数如下表:
(1)从这18名学生中随机选出两名,求两人来自同一个班的概率;
(2)若要求从18位同学中选出两位同学介绍学习经验,设其中来自高二(1)班的人数为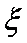

正确答案
见解析
解析
(1)“从这18名同学中随机选出两名,两人来自于同一个班”记作事件A,
则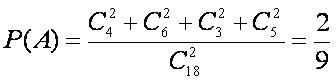
(2)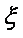
∵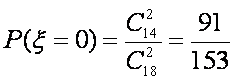
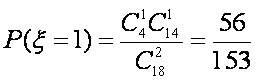
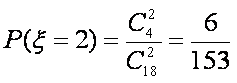
∴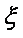
∴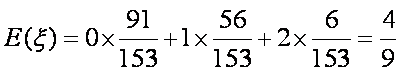
知识点
甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门相同的选法种数为(用数字作答)___
正确答案
30
解析
可先求出所有两人各选修2门的种数

知识点
一次考试共有12道选择题,每道选择题都有4个选项,其中有且只有一个是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错得零分”.某考生已确定有8道题的答案是正确的,其余题中:有两道题都可判断两个选项是错误的,有一道题可以判断一个选项是错误的,还有一道题因不理解题意只好乱猜.请求出该考生:
(1) 得60分的概率;
(2) 所得分数ξ的分布列和数学期望。
正确答案
见解析。
解析
(1) 设“可判断两个选项是错误的”两道题之一选对的为事件A,“有一道题可判断一个选项是错误”选对的为事件B,“有一道题不理解题意”选对的为事件C,
∴P(A)= 


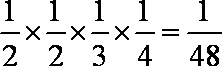
(2) ξ可能的取值为40,45,50,55,60………………………………5分
P(ξ=40)=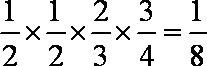
P(ξ=45)=
…………………………………………………………………………7分
P(ξ=50)=
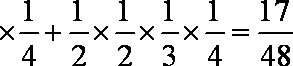
P(ξ=55)=
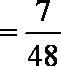
P(ξ=60)=
…………………………………………………………………………10分
(3) Eξ=40×
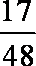
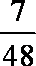
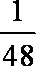
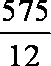
知识点
某工厂生产A,B两种型号的玩具,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种玩具各100件进行检测,检测结果统计如下:
(1)试分别估计玩具A、玩具B为正品的概率;
(2)生产一件玩具A,若是正品可盈利40元,若是次品则亏损5元;生产一件玩具B,若是正品可盈利50元,若是次品则亏损10元,在(I)的前提下,
(i)记X为生产1件玩具A和1件玩具B所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件玩具B所获得的利润不少于140元的概率。
正确答案
见解析。
解析
(1)玩具A为正品的概率约为
玩具B为正品的概率约为
(2)(ⅰ)随机变量





所以,随机变量

(ⅱ)设生产的5件玩具B中正品有

依题意,得 

所以 

设“生产5件玩具B所获得的利润不少于140元”为事件
则 
知识点
某地区有小学150所,中学75所,大学25所. 现采用分层抽样的方法从这些学校中抽取30所学校对学生进行视力调査,应从小学中抽取 所学校,中学中抽取 所学校。
正确答案
18,9
解析
∵分层抽样也叫按比例抽样,由题知学校总数为250所,
所以应从小学中抽取

知识点
盒内有大小相同的10个球,其中3个红色球,3个白色球,4个黑色球.
(1)现从该盒内任取3个球,规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得


(2)甲乙两人做摸球游戏,设甲从该盒内摸到黑球的概率是

正确答案
见解析
解析
解:(1)








经计算得
(2)两人共摸中2次黑球的概率为:




知识点
扫码查看完整答案与解析