- 随机事件及其概率
- 共504题
由不等式





正确答案
解析
平面区域













知识点
甲乙两班进行消防安全知识竞赛,每班出3人组成甲乙两支代表队,首轮比赛每人一道必答题,答对则为本队得1分,答错不答都得0分,已知甲队3人每人答对的概率分别为


(1)求随机变量

(2)求在甲队和乙队得分之和为4的条件下,甲队比乙队得分高的概率。
正确答案
见解析。
解析
(1)




(2)设
则

知识点
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得-1分 . 现从盒内任取3个球
(1)求取出的3个球中至少有一个红球的概率;
(2)求取出的3个球得分之和恰为1分的概率;
(3)设
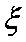
正确答案
见解析
解析
(1)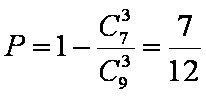
(2)记 “取出1个红色球,2个白色球”为事件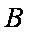
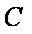
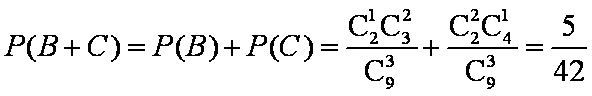
(3)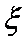
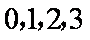
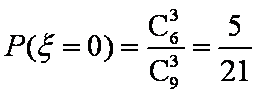
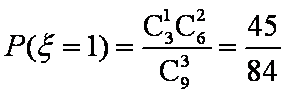
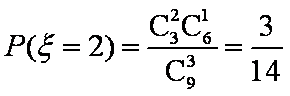
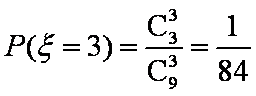
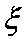
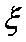
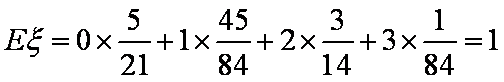
知识点
某机床厂今年年初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元。
(1)写出y与x之间的函数关系式;
(2)从第几年开始,该机床开始盈利(盈利额为正值)。
正确答案
(1)y=
解析
解析:(1)第二年所需维修、保养费用为12+4万元,
第

维修、保养费用成等差数列递增,依题得:


(2)由(1)可知当
解不等式
得
∵

知识点
某校高三(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)频率分布直方图中[80,90)间的矩形的高为_______
(2)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,至少有一份分数在[90,100]之间的概率为_______
正确答案
0.016;0.6
解析
(1)由频率分布的直方图可得成绩落在区间[50,60)内的频率为0.008×10=0.08,
而由茎叶图可得成绩落在区间[50,60)内的只有2个,设样本容量为n,
则有 
故成绩落在[80,90)间的有25﹣21=4,故成绩落在[80,90)间的频率为
故矩形的高为频率除以组距10为
故答案为0.016。
(2)由于故绩落在[80,90)间的有4个,落在[90,100]之间的有2个,
分数在[80,100]之间的试卷中任取两份,所有的取法共有
其中,至少有一份分数在[90,100]之间的取法有

故至少有一份分数在[90,100]之间的概率为 
故答案为0.6
知识点
三分球大赛是NBA全明星周末的比赛项目之一,比赛一共有5个投篮点:底脚对称有两个,45度角对称有两个,另一个在弧顶,每个投篮点有5个球,其中4个橘色球投中了各得1分,最后1个花球投中了得2分,满分为30分,若某球员在任意一个投篮点的5次投篮中,每次投中的概率均为
(1)求该球员在一个投篮点得分为4分的概率;
(2)该球员在五个投篮点投篮结束后,得分为4分的投篮点的个数为X求EX。
正确答案
见解析。
解析
(1)得分为4分,可以前4次中,第5次不中,概率为
或者前4次中2次,第5次中,概率为
所以得分为4分的概率为
(2)得分为4分的投篮点的个数为

知识点
世界园艺博览会将在陕西西安浐灞生态区举行,为了接待来自国内外的各界人士,需招募一批志愿者,要求志愿者不仅要有一定的气质,还需有丰富的人文、地理、历史等文化知识。志愿者的选拔分面试和知识问答两场,先是面试,面试通过后每人积60分,然后进入知识问答。知识问答有A,B,C,D四个题目,答题者必须按A,B,C,D顺序依次进行,答对A,B,C,D四题分别得20分、20分、40分、60分,每答错一道题扣20分,总得分在面试60分的基础上加或减。答题时每人总分达到100分或100分以上,直接录用不再继续答题;当四道题答完总分不足100分时不予录用。
假设志愿者甲面试已通过且第二轮对A,B,C,D四个题回答正确的概率依次是
(1)用X表示志愿者甲在知识问答结束时答题的个数,求X的分布列和数学期 望;
(2)求志愿者甲能被录用的概率。
正确答案
见解析
解析
设某题M答对记为“M”,答错记为“
(1) X的可能取值为2,3,4


X的分布列为:
(2) 志愿者甲能被录用的概率

或
知识点
将一个四棱锥的每个顶点染上一种颜色,并使同一条棱上的两个端点异色,若只有4种颜色可供使用,则不同的染色方法总数有
正确答案
解析
略
知识点
甲、乙两人为了响应政府“节能减排”的号召,决定各购置一辆纯电动汽车,经了解目前市场上销售的主流纯电动汽车,按续驶里程数R(单位:公里)可分为三类车型,A:80≤R<150,B:150≤R<250, C:R≥250,甲从A,B,C三类车型中挑选,乙从B,C两类车型中挑选,甲、乙二人选择各类车型的概率如下表:
若甲、乙都选C类车型的概率为
(1)求

(2)求甲、乙选择不同车型的概率;
(3)某市对购买纯电动汽车进行补贴,补贴标准如下表:
记甲、乙两人购车所获得的财政补贴和为X,求X的分布列。
正确答案
见解析
解析
(1)因为
所以

(2)设“甲、乙选择不同车型”为事件A,
则
答:所以甲、乙选择不同车型的概率是
(3)X 可能取值为7,8,9,10。




所以X的分布列为:
……………………13分
知识点
今年来,随着地方经济的发展,劳务输出大省四川、河南、湖北、安徽等地的部分劳务人员选择了回乡就业,因而使得沿海地区出现了一定程度的用工荒.今年春节过后,沿海某公司对来自上述四省的务工人员进行了统计(见下表):
为了更进一步了解员工的来源情况,该公司

(1)从参加问卷调查的50名务工人员中随机抽取两名,求这两名来自同一个省份的概率;
(2)在参加问卷调查的50名务工人员中,从来自四川、湖北两省的人员中随机抽取两名,用ξ表示抽得四川省务工人员的人数,求ξ的分布列和数学期望。
正确答案
见解析
解析
(1)易得问卷调查中,从上述四省抽取的人数分别为
设“从参加问卷调查

从参加问卷调查的

这两名人




∴
(2)由(1)知,在参加问卷调查的







∴
知识点
扫码查看完整答案与解析










































