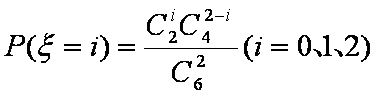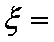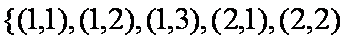- 随机事件及其概率
- 共504题
把一颗质地均匀,四个面上分别标有复数






(1)用



(2)设复数


正确答案
见解析
解析
(1)所有的基本事件个数有






(2)









知识点
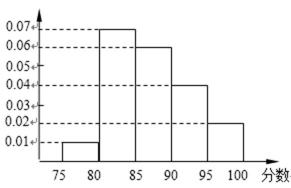
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示。
(1)分别求第3,4,5组的频率;
(2)若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试。
①已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
②学校决定在这6名学生中随机抽取2名学生接受考官D的面试,第4组中有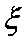
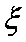
正确答案
见解析。
解析
(1) 第三组的频率为0.06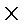
第四组的频率为0.04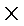
第五组的频率为0.02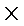
(2)①设M:学生甲和学生乙同时进入第二轮面试
P(M)=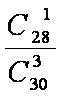

②

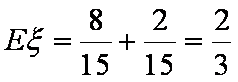
知识点
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数

(1)分别求事件

(2)在两次试验中,记两次得到的数分别为

正确答案
见解析
解析
(1)

(2)
ξ=1,2,4……………………………………………………………5分
由表可知:
所以随机变量
所以
知识点
小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是
(1)求小明没有遇到红灯的概率;
(2)记小明等候的总时间为


正确答案
见解析
解析
解:(1)记“小明没有遇到红灯”为事件A,则

(2)由题可知:



∴
∴
知识点
一个袋中装有大小相同的黑球和白球共9个,从中任取3个球,记随机变量

(1)求袋中白球的个数;
(2)求随机变量
正确答案
见解析
解析
(1)设袋中有白球

即

(2)随机变量

知识点
已知动点


(1)求点

(2)大家知道,过圆上任意一点





(ⅰ)若点




(ⅱ)试探究:若改变曲线


正确答案
见解析
解析
(1)



轨迹方程为
(2)(i)依题意得设
由

同理
因此
即
令


(ii)结论:过抛物线



设点

过
设




化简得

假设

即

比较(*)、(**)得


(如用其它方法,请对照给分)
知识点
在一个盒子中,放有标号分别为1,2,3的三个球,现从这个盒子中,
有放回地先后取得两个球的标号分别为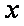
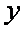
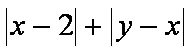
(1)求随机变量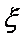
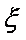
(2)求随机变量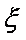
正确答案
见解析。
解析
由题意可得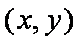
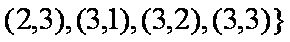
(1)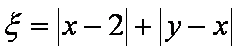
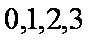
于是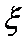
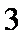
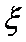
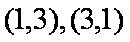
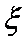
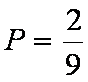
(2)由各个样本赋值可得出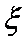
∴可得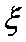
∴随机变量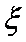
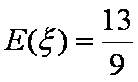
知识点
有A、B、C三个盒子,每个盒子中放有红、黄、蓝颜色的球各一个,所有的球仅有颜色上的区别。
(1)从每个盒子中任意取出一个球,记事件



(2)先从A盒中任取一球放入B盒,再从B盒中任取一球放入C盒,最后从C盒中任取一球放入A盒,设此时A盒中红球的个数为


正确答案
见解析
解析
(1)


(2)


①考虑



















②考虑



















③
所以


知识点
某校在全校学生中开展物理和化学实验操作大比拼活动,活动要求:参加者物理、化学实 验操作都必须参加,有50名学生参加这次活动,评委老师对这50名学生实验操作进行 评分,每项操作评分均按等级采用5分制(只打整数分),评分结果统计如下表:
(1)若随机抽取一名参加活动的学生,求“化学实验得分为4分且物理实验得分为3分”学生被抽取的概率;
(2)从这50名参赛学生中任取1人,其物理实验与化学实验得分之和为ξ,求ξ的数学期望。
正确答案
见解析。
解析
(1)从表中可以看出,“化学实验得分为4分且物理实验得分为3分”学生数为6名,所以“化学实验得分为4分且物理实验得分为3分”学生被抽取的概率为

(2)ξ的所有可能的取值为2,3,4,5,6,7,8,9,10,则ξ的分布列为
∴Eξ=2×









知识点
甲、乙两人进行“石头、剪子、布”游戏,开始时每人拥有3张卡片,每一次“出手”(双方同时):若分出胜负,则负者给对方一张卡片;若不分胜负,则不动卡片,规定:当一人拥有6张卡片或“出手”次数达到6次时游戏结束,设游戏结束时“出手”次数为

正确答案
解析



知识点
扫码查看完整答案与解析