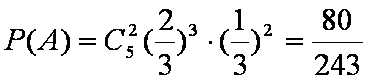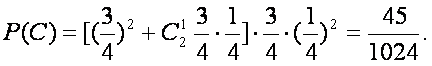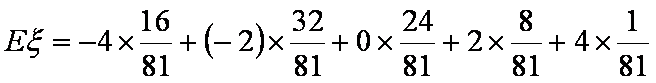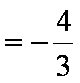- 随机事件及其概率
- 共504题
已知椭圆







(1)求椭圆
(2)设













正确答案
见解析
解析
解:(1)由题意得:


(2)解:设


联立

解得
直线



又直线
因为


直线


令



又因为



化简得:
又C在直线

联立①、② 解得

又

解法二:因为
所以

设

联立


直线



由

知识点
甲、乙两人各射击一次,击中目标的概率分别是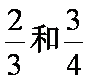
(1)求甲射击5次,有两次未击中目标的概率;
(2)假设某人连续2次未击中目标,则中止其射击,求乙恰好射击5次后,被中止射击的概率。
正确答案
见解析
解析
解:(1)设“甲射击5次,有两次未击中目标”
为事件A,则
(2)设“乙恰好射击5次后,被中止射击”为事件C,由于乙恰好射击5次后被中止射击,所以必然是最后两次未击中目标,第一次及第二次至多次有一次未
击中目标,则
知识点
学校游园活动有这样一个游戏项目:甲箱子里装有





(1)求在
①摸出
②获奖的概率;
(2)求在


正确答案
见解析
解析
解:(1)①解:设“在

②解:设“在1次游戏中获奖”为事件


且

(2)解:由题意可知



所以
所以

知识点
甲乙两队参加奥运知识竞赛,每队三人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为

(1)若用

(2)用



正确答案
见解析
解析
(1)由题意知,





所以
故
(2)用







∴
知识点
一个袋中有大小相同的标有1,2,3,4,5,6的6个小球,某人做如下游戏,每次从袋中拿一个球(拿后放回),记下标号。若拿出球的标号是3的倍数,则得1分,否则得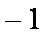
(1)求拿4次至少得2分的概率;
(2)求拿4次所得分数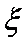
正确答案
见解析
解析
解(1)设拿出球的号码是3的倍数的为事件A,则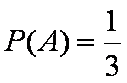
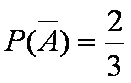
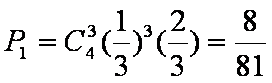
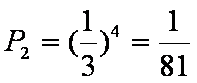
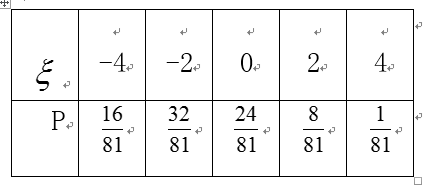
(2)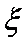
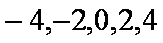
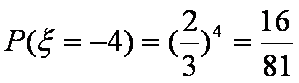
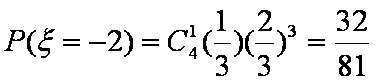
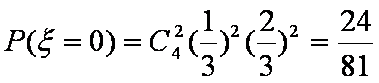
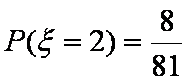

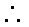
知识点
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为

(1)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为

(2)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
正确答案
见解析。
解析
(1)由已知得,张三中奖的概率为

记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,
因为






(2)设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,
则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),
选择方案乙抽奖累计得分的数学期望为E(3X2)。
由已知可得,X1~

所以E(X1)=2×


从而E(2X1)=2E(X1)=

若


若


若


综上所述:当


知识点
某班主任对全班30名男生进行了作业量多少的调查,数据如下表:
该班主任据此推断男生喜欢玩电脑游戏与认为作业量的多少有关,这种推断犯错误的概率不超过____________
正确答案
0.050
解析

∴错误的概率不超过0.050。
知识点
某学校为响应省政府号召,每学期派老师到各个民工子弟学校支教,以下是该学校
根据上表信息解答以下问题:
(1)从该学校任选两名老师,用





(2)从该学校任选两名老师,用


正确答案
见解析。
解析
(1) 函数


则必有

所以,
当

(2) 从该学校任选两名老师,用
则

于是


从而


知识点
某产品的三个质量指标分别为x, y, z, 用综合指标S = x + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 先从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品中, 随机抽取两件产品,设“取出的2件产品的综合指标之差的绝对值”为随机变量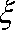
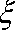
正确答案
见解析。
解析
(1)计算10件产品的综合指标S,如下表:
其中S≤4的有A1,A2,A4,A5,A7,A9,共6件,故该样本的一等品率为=0.6,从而可估计该批产品的一等品率为0.6………………5分
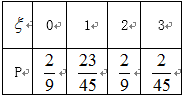
(2) 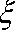
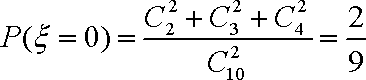
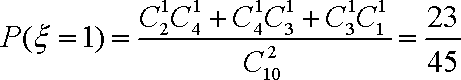
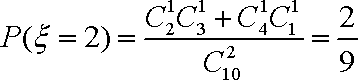
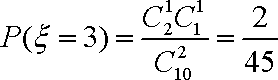
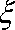
所以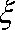
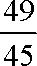
知识点
从0,1,2,3,4,5这6个数字中任意取4个数字组成一个没有重复数字的四位数,这个数能被3整除的概率为____________
正确答案
解析
从0,1,2,3,4,5这6个数字中任意取4个数字组成没有重复数字的四位数,共有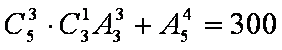
1,2,4,5; 0,3,4,5;0,2,3,4;0,1,3,5;0,1,2,3组成,所以能被3整除的有:
∴这个数能被3整除的概率为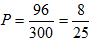
知识点
扫码查看完整答案与解析