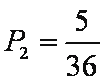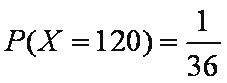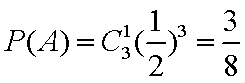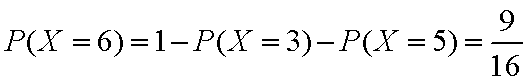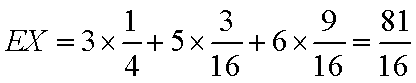- 随机事件及其概率
- 共504题
在雅礼中学组织的“雅礼杯”篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是

(1)求3次投篮的人依次是甲、甲、乙的概率;
(2)若投篮命中一次得1分,否则得0分. 用ξ表示甲的总得分,求ξ的分布列和数学期望。
正确答案
见解析。
解析
(1)记 “3次投篮的人依次是甲、甲、乙” 为事件A.
由题意, 得
答:3次投篮的人依次是甲、甲、乙的概率是
(2)由题意,ξ的可能取值为0,1,2,3,则




所以,


知识点
某班同学利用国庆节进行社会实践,对

(1)补全频率分布直方图并求
(2)从年龄段在

正确答案
见解析。
解析
(1)第二组的频率为1-(0.04+0.04+0.03+0.02+0.02)×5=0.3.所以高为
第一组人数为

又题可知,第二组的频率0.3,第二组人数为

第四组的频率0.03×5=0.15,所以第四组人数为

(2)因为








知识点
某中学在高三开设了4门选修课,每个学生必须且只需选修1门选修课。对于该年级的甲、乙、丙3名学生,回答下面的问题:
(1)求这3名学生选择的选修课互不相同的概率;
(2)某一选修课被这3名学生选修的人数的数学期望。
正确答案
见解析。
解析
(1) 3名学生选择的选修课互不相同的概率: 
(2)设某一选修课被这3名学生选择的人数为




所以
数学期望
知识点
某旅游景点为了增加人气,吸引游客,特推出一系列活动.其中有一项活动是:凡购买该景点门票的游客,可参加一次抽奖:掷两枚6个面分别标有数字1,2,3,4,5,6的正方体骰子,点数之和为12点获一等奖,奖品价值120元;点数之和为11点或10点获二等奖,奖品价值60元;点数之和为9点或8点获三等奖,奖品价值20元;点数之和小于8点的不得奖.
(1)求同行的两位游客中一人获一等奖、一人获二等奖的概率;
(2)设一位游客在该景点处获奖的奖品价值为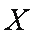
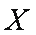

正确答案
见解析。
解析
(1)一位游客获一等奖的概率为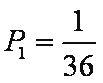
故 两位游客中一人获一等奖、一人获二等奖的概率为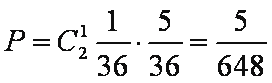
(2)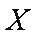
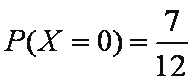
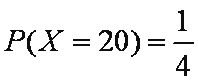
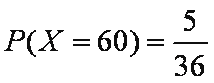
∴ 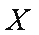
∴ 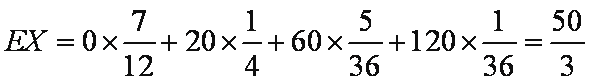
知识点
甲、乙两人在一场五局三胜制的象棋比赛中,规定甲或乙无论谁先赢满三局就获胜,并且比赛就此结束.现已知甲、乙两人每比赛一局甲取胜的概率是

(1)比赛以甲3胜1而结束的概率;
(2)比赛以乙3胜2而结束的概率;
(3)设甲获胜的概率为a,乙获胜的概率为b,求a:b的值。
正确答案
见解析。
解析
(1) 比赛以甲3胜1而结束,则第四局一定甲胜,前三局中甲胜两局,
∴所求概率为:
答:比赛以甲3胜1而结束的概率为
(2) 比赛以乙3胜2而结束,则第五局一定乙胜,前四局中乙胜两局,
∴所求概率为: 
答:比赛以乙3胜2而结束的概率为
(3)甲先胜3局的情况有3种:3胜无败,3胜1败,3胜2败.,则其概率分别为




于是甲获胜的概率
∴乙获胜的概率


知识点
有甲、乙两种相互独立的预防措施可以降低某地区某灾情的发生,单独采用甲、乙预防措施后,灾情发生的概率分别为0.08和0.10,且各需要费用60万元和50万元,在不采取任何预防措施的情况下发生灾情的概率为0.3.如果灾情发生,将会造成800万元的损失,(设总费用=采取预防措施的费用+可能发生灾情损失费用)
(1)若预防方案允许甲、乙两种预防措施单独采用,他们各自总费用是多少?
(2)若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用,请确定预防方案使总费用最少的那个方案。
正确答案
见解析
解析
解(1)若单独采用甲预防措施,可能发生灾情的损失费用的期望值为
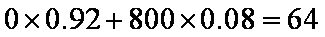
若单独采用乙预防措施,可能发生灾情的损失费用的期望值为
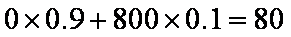
所以,单独采用甲预防措施的总费用为124万元,单独采用乙预防措施的总费用为130万元,
(2)若实施联合采用方案,设可能发生灾情的损失费用为X,则X = 0和800,
且 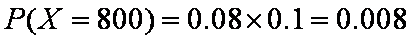
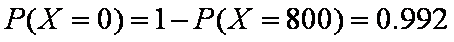
所以,可能发生灾情的损失费用的期望值为6.4万元,因此总费用为116.4万元。
若不采取措施,则可能发生灾情的损失费用的期望值为
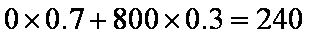
可知此时的总费用为240万元,
综上,选择联合预防措施的方案总费用最少,
知识点
甲、乙两位同学各有3张卡片,现以投掷均匀硬币的形式进行游戏,当出现正面朝上时甲赢得乙一张卡片,否则乙赢得甲一张卡片.规定掷硬币的次数达6次时,或在此前某人已赢得所有卡片时游戏终止。设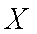
(1)求第三次掷硬币后甲恰有4张卡片的概率;
(2)求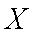
正确答案
见解析
解析
解:(1)记“第三次掷硬币后甲恰有4张卡片”为事件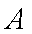
(2)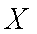
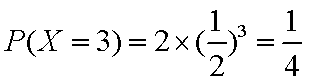
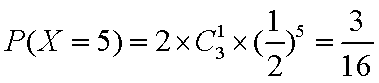
分布列为:
知识点
某班甲、乙两名学同参加100米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:
(1)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率。
(2)后来经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5 ]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率。
正确答案
(1)
(2)
解析
(1)设事件A为:甲的成绩低于12.8,事件B为:乙的成绩低于12.8,
则甲、乙两人成绩至少有一个低于12.8秒的概率为
(2)设甲同学的成绩为x,乙同学的成绩为y,
则|x-y|<0.8, 得-0.8+x<y<0.8+x
如图阴影部分面积即为3×3-2.2×2.2=4.16
则P(|x-y|<0.8)=P(-0.8+x<y<0.8+x)=
知识点
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为

(1)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为

(2)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
正确答案
见解析。
解析
(1)由已知得,张三中奖的概率为,李四中奖的概率为
记“这2人的累计得分X≤3”的事件为A,
则事件A的对立事件为“X=5”,
因为P(X=5)=×


(2)设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,
则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),
选择方案乙抽奖累计得分的数学期望为E(3X2)。
由已知可得,X1~B,X2~B
所以E(X1)=2×=,E(X2)=2×
从而E(2X1)=2E(X1)=,E(3X2)=3E(X2)=6
若E(2X1)>E(3X2),则
若E(2X1)<E(3X2),则
若E(2X1)=E(3X2),则
综上所述,当
当
当
知识点
某校政教处为检查各班落实学校“学生素养五十条”的规定情况,从各班抽取了一批学生进行测试,全部学生参加了“理论部分”和“模拟现场”两项测试,成绩均分为A,B,C,D,E五个等级. 某考场考生两项测试成绩的数据统计如下图所示,其中“理论部分”科目测试成绩为B的考生有20人.
(1)求该考场考生中“模拟现场”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分.
(i)求该考场考生 “理论部分”科目的平均分;
(ii)若该考场共有10人得分大于7分,其中有2人10分,2人9分,6人8分. 从这10人中随机抽取两人,求两人成绩之和的分布列和数学期望.
正确答案
见解析。
解析
(1)因为“理论部分”科目中成绩等级为B的考生有20人,
所以该考场有

(2)(i) 求该考场考生“理论部分”科目的平均分为

法二:
(ii)设两人成绩之和为




所以
……………11分
所以


知识点
扫码查看完整答案与解析