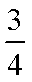- 随机事件及其概率
- 共504题
某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,如下表所示。
已知这100位顾客中一次购物量超过8件的顾客占55%。
(1)确定x,y的值,并求顾客一次购物的结算时间X的分布列与数学期望;
(2)若某顾客到达收银台时前面恰有2位顾客需结算,且各顾客的结算相互独立,求该顾客结算前的等候时间不超过2.5分钟的概率,(注:将频率视为概率)
正确答案
见解析
解析
解析:(1)由已知,得25+y+10=55,x+30=45,所以x=15,y=20。
该超市所有顾客一次购物的结算时间组成一个总体,所收集的100位顾客一次购物的结算时间可视为总体的一个容量为100的简单随机样本,将频率视为概率得

所以


(2)记




知识点
某高校在2011年自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第1组[75,80),第2组[80,85), 第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示。
(1)分别求第3,4,5组的频率;
(2) 若该校决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试,
(ⅰ) 已知学生甲和学生乙的成绩均在第三组,求学生甲和学生乙同时进入第二轮面试的概率;
(ⅱ) 学校决定在这6名学生中随机抽取2名学生接受考官D的面试,设第4组中有

正确答案
见解析
解析
解:(1)第三组的频率为0.06
第四组的频率为0.04
第五组的频率为0.02
(2)
(ⅰ)设M:学生甲和学生乙同时进入第二轮面试
P(M)=

(ⅱ)

知识点
第11届全国人大五次会议于2012年3月5日至3月14日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名女记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语。
(1)根据以上数据完成以下2×2列联表:
并回答能否在犯错的概率不超过0.10的前提下认为性别与会俄语有关?
参考公式:
参考数据:
(2)若从会俄语的记者中随机抽取3人成立一个小组,则小组中既有男又有女的概率是多少?
(3)若从14名女记者中随机抽取2人担任翻译工作,记会俄语的人数为

正确答案
见解析。
解析
(1)如下表:

假设:是否会俄语与性别无关.由已知数据可求得
所以在犯错的概率不超过0.10的前提下不能判断会俄语与性别有关;
(2)
(3)会俄语的人数


所以

知识点
在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于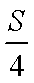
正确答案
解析
解析:在面积为S的△ABC的边AB上任取一点P,则基本事件空间为线段AB的长度。设点D为边AB的一个四等分点(最靠近B的那个),若使△PBC的面积大于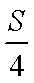
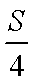
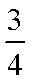
知识点
盒子中装有四张大小形状均相同的卡片,卡片上分别标有数

(1)分别求事件

(2)在两次试验中,记两次得到的数分别为

正确答案
见解析。
解析
(1)

(2)
ξ=1,2,4……………………………………………………………5分
由表可知:
所以随机变量
所以
知识点
下图是预测到的某地5月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择5月1日至5月13日中的某一天到达该市,并停留2天
(1)求此人到达当日空气质量优良的概率;
(2)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望
(3)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明).
正确答案
(1)
解析
(1)由于1-13号共有6天的空气质量指数小于100,所以即可求出此人到达当日空气质量优良的概率.
(2)由于X是此人停留期间空气质量优良的天数,所以有三种情况:

(3)由题意可得判断从哪天开始连续三天的空气质量指数方差最大,就是观察三天的波动最大的情况即可.
设
依据题意P(


(1)设B表示事件“此人到达当日空气质量优良”
P(B)=
(2)X的所有可能取值为0,1,2
P(X=0)=
P(X=2)=
∴X的分布列为
8分
∴X的数学期望为E(X)=
(3)从5月5日开始连续三天的空气质量指数方差最大. 13分
知识点
某产品的三个质量指标分别为x, y, z, 用综合指标S = x + y + z评价该产品的等级. 若S≤4, 则该产品为一等品. 先从一批该产品中, 随机抽取10件产品作为样本, 其质量指标列表如下:
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样品中, 随机抽取两件产品,设“取出的2件产品的综合指标之差的绝对值”为随机变量

正确答案
见解析。
解析
(1)计算10件产品的综合指标S,如下表:
其中S≤4的有A1,A2,A4,A5,A7,A9,共6件,故该样本的一等品率为=0.6,从而可估计该批产品的一等品率为0.6
(2) 




所以
知识点
现对某市工薪阶层关于“楼市限购政策”的态度进行调查,随机抽查了50人,他们月收入的频数分布及对“楼市限购政策”赞成人数如下表:
(1)根据以上统计数据填写下面2×2列联表,并回答是否有99%的把握认为月收入以5500元为分界点对“楼市限购政策” 的态度有差异?
(2) 若从月收入在[15,25) ,[25,35)的被调查对象中各随机选取两人进行调查,记选中的4人中不赞成“楼市限购政策”人数为

(参考公式:

参考值表:
正确答案
见解析。
解析
(1)根据题目得2×2列联表:
假设月收入以5500为分
假设不成立.
所以没有99%的把握认为月收入以5500为分界点对“楼市限购政策”的态度有差异.
(2)
所以
所以
知识点
某校设计了一个实验学科的能力考查方案:考生从







(1)求考生甲能通过该实验学科能力考查的概率;
(2)记所抽取的




(3)试用统计知识分析比较甲、乙考生在该实验学科上的能力水平。
正确答案
见解析。
解析
本小主要考查概率、统计等基础知识,考查数据处理能力、运算求解能力以及应用数学知识分析和解决实际问题的能力,满分13分。
(1)记“考生甲能通过该实验学科能力考查”为事件
则基本事件总数


所以
答:考生甲能通过该实验学科能力考查的概率为
(2)









(3设考生乙能正确完成的题数为




即






记“考生乙能通过该实验学科能力考查”为事件
则
(1)因为
(2)因为
(3)因为
(4)给出结论:甲在该实验学科上的能力水平较强. ……13分
知识点
某教研机构准备举行一次高中数学新课程研讨会,拟邀请50名使用不同版本的一线教师参加,使用不同版本教材的教师人数如下表所示:
(1)从这50名教师中随机选出2名教师发言,求第一位发言的教师所使用版本是北大师大版的概率;
(2)设使用北师大版的5名教师中有3名男教师,2名女教师,使用苏教版的10名教师中有6名男教师,4名女教师,若从这15名教师中随机选出3名教师发言,求选到用苏教版的女教师人数的分布列和期望。
正确答案
见解析。
解析
(1)法一:只考虑第一位发言的老师,则
法二:
(2 )设选到用苏教版的女教师的人数为


选到用苏教版的女教师的人数
知识点
扫码查看完整答案与解析