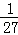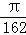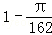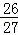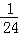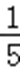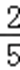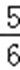- 随机事件及其概率
- 共504题
在棱长为3的正方体内任取一点P,则点P到该正方体的六个面的距离的最小值不大于1的概率为( )
正确答案
解析
由题意,符合点P到该正方体的六个面的距离的最小值不大于1的区域是以正方体的中心为中心棱长为1的正方体外部,根据几何概型公式可得点P到该正方体的六个面的距离的最小值不大于1的概率为1﹣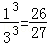
故选:D.
知识点
9.平面上画了一


正确答案
解析
由于平行线相距



知识点
16.北师大和华师大两所高校,准备从2014年毕业生中各选派1名优秀毕业生去汶川和玉树地区从事教育教学工作,其中北师大有2名男生1名女生报名,华师大有1名男生和2名女生报名。
(1)若从两所学校报名的学生中各任选一名,写出所有可能的结果,并求选出的2名学生性别相同的概率;
(2)若从报名的6名学生中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率。
正确答案
见解析。
解析
记北师大的学生为





(1)由题意知从两所学校报名的学生中各任选一名,写出所有可能的结果为(

















所以选出的2名学生性别相同的概率
(2) 若从报名的6名学生中任选2名,写出所有可能的结果(





























知识点
调查表明,中年人的成就感与收入、学历、职业的满意度的指标有极强的相关性,现
将这三项的满意度指标分别记为x,y,z,并对它们进行量化:0表示不满意,1表示基本满意,2表示满意,再用综合指标w=x+y+z的值评定中年人的成就感等级:若w≥4,则成就感为一级;若2≤w≤3,则成就感为二级;若0≤w≤1,则成就感为三级,为了了解目前某群体中年人的成就感情况,研究人员随机采访了该群体的10名中年人,得到如下结果:
人员编号 A1 A2 A3 A4 A5
(x,y,z) (1,1,2) (2,1,1) (2,2,2) (0,1,1) (1,2,1)
人员编号 A6 A7 A8 A9 A10
(x,y,z) (1,2,2) (1,1,1) (1,2,2) (1,0,0) (1,1,1)
(1)在这10名被采访者中任取两人,求这两人的职业满意度指标相同的概率;
(2)从成就感等级是一级的被采访者中任取一人,其综合指标为a,从成就感等级不是一级的被采访者中任取一人,其综合指标为b,记随机变量X=a﹣b,求X的分布列及其数学期望。
正确答案
见解析。
解析
(1)设事件A为“从10名被采访者中随机抽取两人,他们的职业满意度指标相同”,从10名被采访者中随机抽取两人的所有可能结果数为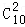
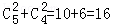
(2)由已知得随机变量X的所有可能取值为:1,2,3,4,5,分别求出相应的概率,由此能求出X的分布列及其数学期望。
(1)设事件A为“从10名被采访者中随机抽取两人,他们的职业满意度指标相同”。
职业满意度指标为0的有:A9;
职业满意度指标为1的有:A2,A4,A5,A7,A10,
职业满意度指标为2的有:A1,A3,A6,A8。
从10名被采访者中随机抽取两人的所有可能结果数为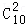
职业满意度指标相同的所有可能结果数为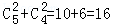
所以他们的职业满意度指标相同的概率P(A)=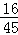
(2)计算10名被采访者的综合指标,可得下表:
人员编号 A1 A2 A3 A4 A5 A6 A7 A8 A9 A10
综合指标 4 4 6 2 4 5 3 5 1 3
其中成就感是一级的(w≥4)有:A1、A2、A3、A5、A6、A8,共6名,
成就感不是一级的(w<4)有A4、A7、A9、A10,共4名。
随机变量X的所有可能取值为:1,2,3,4,5.(6分)
P(X=1)=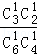
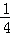
P(X=2)=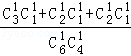
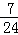
P(X=3)=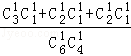
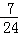
P(X=4)=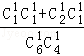
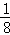
P(X=5)=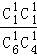
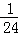
所以X的分布列为
X 1 2 3 4 5
P 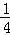
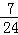
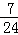
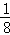
(12分)
所以E(X)=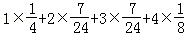
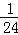
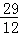
知识点
17.某电视台一档娱乐选秀节目2013-2014年度更新了新规则,制定了由一轮晋级二轮的规则如下:每名选手准备三个节目,按顺序表演.第一个节目有专业评委全票通过,则直接晋级第二轮,否则表演第二个和第三个节目;第二个节目由专业评委投票是否通过,第三个节目由现场观众投票是否通过.若第二个节目获得专业评委三分之二及以上票数通过且第三个节目得到现场观众三分之二及以上票数以上,则晋级第二轮;若第二个节目没有获得专业评委三分之二票数通过,但第三个节目获得现场观众全票通过,也同样晋级到第二轮,否则被淘汰.某位选手估计自己三个节目的通过概率如下表:
若晋级,后面的节目不需要再表演,也不考虑中途自己退出比赛的情况.
(1)求该选手晋级表演节目数
(2)求该选手晋级的概率。
正确答案
见解析。
解析
(1)由题意可知随机变量

表演节目数
(2)该选手晋级可以是第一个节目专业评委全票通过;也可以是第二个节目获得专业评委三分之二及以上票数通过且第三个节目得到现场观众三分之二及以上票数以上;或者是第二个节目没有获得专业评委三分之二票数通过,但第三个节目获得现场观众全票通过,设该选手晋级的事件为A,
则
知识点
某校从参加某次知识竞赛的同学中,选取60名同学将其成绩(百分制,均为整数)分成6组后,得到部分频率分布直方图(如图),观察图中的信息,回答下列问题。
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)根据频率分布直方图,估计本次考试的平均分;
(3)若从60名学生中随机抽取2人,抽到的学生成绩在[40,70)记0分,抽到的学生成绩
在[70,100]记1分,用X表示抽取结束后的总记分,求X的分布列和数学期望。
正确答案
见解析
解析
解:(1)设分数在
则有
所以频率分布直方图如图所示:
(2)平均分为:
(3)学生成绩在[40,70)的有0.4×60=24人,在[70,100]的有0.6×60=36人,
且X的可能取值是0,1,2。
则



所以X的分布列为:
所以EX=0×




知识点
一个口袋中有



(1)试用含

(2)若
(3)记三次摸球恰有一次中奖的概率为


正确答案
见解析
解析
(1)一次摸球从

其中两球颜色相同有
∴一次摸球中奖的概率
(2)若


(3)设一次摸球中奖的概率是
则三次摸球中恰有一次中奖的概率是
∵
∴


∴当

由
∴
知识点
8.平面上画了一


正确答案
解析
由于平行线相距



知识点
某单位实行休年假制度三年以来,50名职工休年假的次数进行的调查统计结果如下表所示:
根据上表信息解答以下问题:
(1)从该单位任选两名职工,用






(2)从该单位任选两名职工,用


正确答案
见解析。
解析
(1) 函数




所以,
当




所以
(2)从该单位任选两名职工,用


于是


从而


知识点
8.若实数x,y满足的约束条件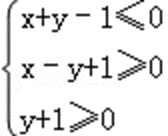
正确答案
解析
画出不等式组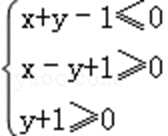
∵函数z=2ax+by在点(2,﹣1)处取得最大值,
∴直线z=2ax+by的斜率k=
∵一颗骰子投掷两次分别得到点数为(a,b),则这样的有序整数对共有6×6=36个
其中2a≤b的有(1,1),(1,2),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)共30个,
则函数z=2ax+by在点(2,﹣1)处取得最大值的概率为 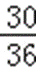
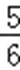
知识点
扫码查看完整答案与解析