- 随机事件及其概率
- 共504题
19.某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如下:
(1)试分别估计芯片甲,芯片乙为合格品的概率;
(2)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(1)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.
正确答案
见解析。
解析
(1)芯片甲为合格品的概率约为
芯片乙为合格品的概率约为
(2)(ⅰ)随机变量X的所有取值为90,45,30,-15




所以,随机变量X的分布列为:
(ⅱ)设生产的5件芯片乙中合格品n件,则次品有5﹣n件.
依题意,得 50n﹣10(5﹣n)≥140,解得 
设“生产5件芯片乙所获得的利润不少于140元”为事件A,
则 
知识点
8.定义区间(a,b),[a,b),(a,b],[a,b]的长度均为d=b-a,多个区间并集的长度为各区间长度之和,例如,(1,2)∪[3,5)的长度d=(2-1)+(5-3)=3.用[x]表示不超过x的最大整数,记{x}=x-[x],其中x∈R.设f(x)=[x]·{x},g(x)=x-1,当0≤x≤k时,不等式f(x)<g(x)的解集区间的长度为5,则k=( )
正确答案
解析
f(x)=[x]·{x}=[x]·(x-[x])=[x]x-[x]2,由f(x)<g(x),得[x]x-[x]2<x-1,即
知识点
7.执行右图程序框图,如果输入的

正确答案
解析
若x=t=2,
则第一次循环,1≤2成立,则M= 
第二次循环,2≤2成立,则M= 
此时3≤2不成立,输出S=7,
故选:D.
知识点
18.某校从参加某次知识竞赛的同学中,选取






(1)求分数在
(2)从频率分布直方图中,估计本次考试成绩的中位数;
(3)若从第1组和第6组两组学生中,随机抽取2人,求所抽取2人成绩之差的绝对值大于10的概率。
正确答案
(1)

解析
(1)分数在[70,80)内的频率为1﹣(0.010+0.015+0.015+0.025+0.005)×10=0.3,
∴小矩形的高为0.030,补全频率分布直方图如图:
(2)由频率频率分布直方图知前三组的频率之和为0.1+0.15+0.15=0.4,
∴中位数在第四组,设中位数为70+x,则0.4+0.030×x=0.5⇒x=
∴数据的中位数为70+

(3)第1组:
第6组:
共有36个基本事件,满足条件的有18个,所以概率为
知识点
17.工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别

(1)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为




(3)假定
正确答案
见解析。
解析
方法一:(1)无论以怎样的顺序派出人员,任务不能被完成的概率都是
(2)当依次派出的三个人各自完成任务的概率分别为

所需派出的人员数目的均值(数学期望)EX是
(3)(方法一)由(II)的结论知,当以甲最先、乙次之、丙最后的顺序派人时,
根据常理,优先派出完成任务概率大的人,可减少所需派出的人员数目的均值。
下面证明:对于


事实上,
即(*)成立。
方法二:(i)可将(2)中所求的EX改写为


(ii)也可将(2)中所求的EX改写为


序综合(i)(ii)可知,当
知识点
10.若从区间

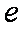
正确答案
解析
略。
知识点
10.已知数列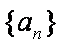
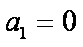
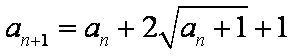
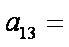
正确答案
解析
由an+1=an+2
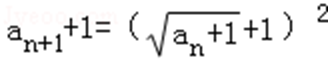
∴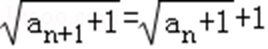
∴{
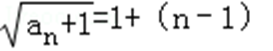
∴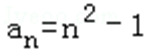
知识点
13.从6名志愿者中选出4人分别从事翻译、导游、导购、保洁四项不同的工作,若其中甲、乙两名志愿者不能从事翻译工作,则选派方案共有________。
正确答案
240种。
解析
根据题意,由排列可得,从6名志愿者中选出4人分别从事四项不同工作,有A=360种不同的情况,其中包含甲从事翻译工作,有A=60种,乙从事翻译工作,有A=60种,若其中甲、乙两名志愿者都不能从事翻译工作,则选派方案共有360-60-60=240种。
知识点
17.某超市从2015年甲、乙两种酸奶的日销售量(单位:箱)的数据中分别随机抽取100个, 并按
假设甲、乙两种酸奶独立销售且日销售量相互独立
(1)写出频率分布直方图(甲)中


(2)估计在未来的某一天里,甲、乙两种酸奶的销售量恰有一个高于20箱且另一个不高于20箱的概率;
(3)设

正确答案
见解析。
解析
(1)

(2)设事件
事件
事件
不高于20箱. 则

所以 
(3)由题意可知,




所以
所以 

另解:由题意可知
所以 

知识点
18.为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:
每名快递员完成一件货物投递可获得的劳务费情况如下:
甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为

(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.
正确答案
(1)平均数为36,众数为33
(2)E(X)=165.5元
(3)甲公司被抽取员工该月收入4860元,乙公司被抽取员工该月收入4965元.
解析
(1)甲公司员工A投递快递件数的平均数为36,众数为33.
(2)设
当





(3)根据图中数据,可估算甲公司被抽取员工该月收入4860元,乙公司被抽取员工该月收入4965元.
知识点
扫码查看完整答案与解析



















