- 随机事件及其概率
- 共504题
8.将4名志愿者分配给特奥会三个不同项目,每个项目至少分配一名自愿者,那么不同的分配方案有( )种。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售.如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式;
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
以100天记录的各需求量的频率作为各需求量发生的概率.
①若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列、数学期望及方差;
②若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
正确答案
解:(1)当日需求量n≥16时,利润y=80.
当日需求量n<16时,利润y=10n-80.
所以y关于n的函数解析式为
y=
(2)①X可能的取值为60,70,80,并且P(X=60)=0.1,P(X=70)=0.2,P(X=80)=0.7.
X的分布列为
X的数学期望为
EX=60×0.1+70×0.2+80×0.7=76.
X的方差为DX=(60-76)2×0.1+(70-76)2×0.2+(80-76)2×0.7=44.
②答案一:
花店一天应购进16枝玫瑰花.理由如下:
若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的分布列为
Y的数学期望为EY=55×0.1+65×0.2+75×0.16+85×0.54=76.4.
Y的方差为DY=(55-76.4)2×0.1+(65-76.4)2×0.2+(75-76.4)2×0.16+(85-76.4)2×0.54=112.04.
由以上的计算结果可以看出,DX<DY,即购进16枝玫瑰花时利润波动相对较小.
另外,虽然EX<EY,但两者相差不大.
故花店一天应购进16枝玫瑰花.
答案二:
花店一天应购进17枝玫瑰花.理由如下:
若花店一天购进17枝玫瑰花,Y表示当天的利润(单位:元),那么Y的分布列为
Y的数学期望为EY=55×0.1+65×0.2+75×0.16+85×0.54=76.4.
由以上的计算结果可以看出,EX<EY,即购进17枝玫瑰花时的平均利润大于购进16枝时的平均利润.故花店一天应购进17枝玫瑰花.
解析
解析已在路上飞奔,马上就到!
知识点
17.在西部大开发中,某市的投资环境不断改善,综合竞争力不断提高,今年一季度先后有甲、乙、丙三个国际投资考察团来到该市,独立地对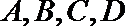
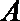
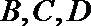
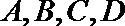
(1)求甲考察团决定到该市投资的概率;
(2)假设乙、丙考察团决定到该市投资的概率都与甲相等,记甲、乙、丙三个考察团中决定到该市投资的考察团个数为随机变量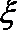
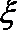
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.掷两颗均匀的骰子得两数,则事件“两数之和大于4”的概率为________。(结果用最简分数表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 随着人们对雾霾环境关注度的提高,绿色低碳出行越来越受到市民重视,为此成都市建立了公共自行车服务系统,市民凭本人二代身份证到公共自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2 分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过一小时的概率分别是0.5和0.6;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.2.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量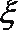
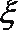
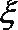
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.甲、乙等五名志愿者被分配到上海世博会中国馆.英国馆.澳大利亚馆.俄罗斯馆四个不同的岗位服务,每个岗位至少一名志愿者,则甲.乙两人各自独立承担一个岗位工作的分法共有( )种。(用数字做答)
正确答案
72
解析
解析已在路上飞奔,马上就到!
知识点
17.本题(1)、(2)两个必答题。
(1)选修4-2 矩阵与变换
曲线

①求实数
②求M的逆矩阵M-1
(2)选修4-4 坐标系与参数方程
已知直线




正确答案
(1)
代入新曲线
解得
由逆矩阵公式得
(2)解法一:将圆的参数方程化为普通方程,
得
直线
即
圆心到直线的距离
所以
解法二:直线的参数方程为
将圆的参数方程化为普通方程,得
将直线的参数方程代入圆的普通方程得:

即

解析
解析已在路上飞奔,马上就到!
知识点
16.PISA2012测试上海样本中有42所一般普通高中和32所中等职业技术学校,为了某项问题的研究,用分层抽样的方法需要从这两类学校中在抽取一个容量为37的样本,则应该抽取一般普通高中学校数为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.口袋中有大小、质地均相同的9个球,4个红球,5个黑球,现在从中任取4个球。
(1)求取出的球颜色相同的概率;
(2)若取出的红球数设为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.10张奖券中只有3张有奖,5个人购买,每人一张,至少有1人中奖的概率是_______________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


























