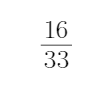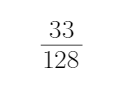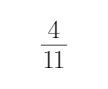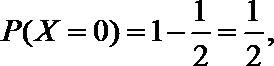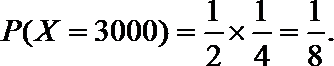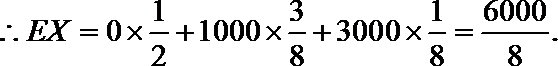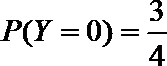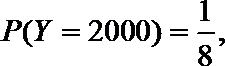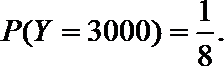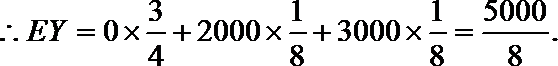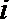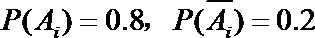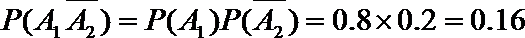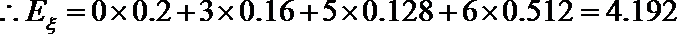- 随机事件及其概率
- 共504题
17. 某学校数学兴趣小组有10名学生,其中有4名女同学;英语兴趣小组有5名学生,其中有3名女学生,现采用分层抽样方法(层内采用不放回简单随机抽样)从数学兴趣小组、英语兴趣小组中共抽取3名学生参加科技节活动。
(1)求从数学兴趣小组、英语兴趣小组各抽取的人数;
(2)求从数学兴趣小组抽取的学生中恰有1名女学生的概率;
(3)记

正确答案
解:(1)抽取数学小组的人数为2人;英语小组的人数为1人;
(2)

(3)


解析
解析已在路上飞奔,马上就到!
知识点
16.一个袋中装有大小相同的黑球和白球共9个,从中任取2个球,记随机变量

(Ⅰ)求袋中白球的个数;
(Ⅱ)求随机变量
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.样本容量为200的频率分布直方图如右图所示,根据样本频率分布直方图估计, 样本数据落在

正确答案
64; 0.4
解析
解析已在路上飞奔,马上就到!
知识点
6. 某地举行一次民歌大奖赛,六个省各有一对歌手参加决赛,现要选出4名优胜者,则选出的4名选手中恰有且只有两个人是同一省份的歌手的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.某人随机地在如图所示正三角形及其外接圆区域内部投针(不包括三角形边界及圆的边界),则针扎到阴影区域(不包括边界)的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.甲、乙两篮球运动员进行定点投篮,每人各投4个球,甲投篮命中的概率为

(I)求甲至多命中2个且乙至少命中2个的概率;
(II)若规定每投篮一次命中得3分,未命中得

正确答案
(Ⅰ)设“甲
“乙至少命中两个球”为事件B,
由题意得:
∴甲至多命中2个球且乙至少命中2个球的概率为:
(Ⅱ)η=-4,0,4,8,12,分布列如下:
解析
解析已在路上飞奔,马上就到!
知识点
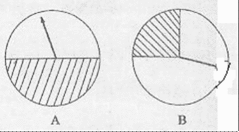
16.如图,两个圆形转盘A,B,每个转盘阴影部分各占转盘面积的

(1)记先转A转盘最终所得积分为随机量X,则X的取值分别是多少?
(2)如果你参加此活动,为了赢得更多的积分,你将选择先转哪个转盘?请说明理由。
正确答案
(1)X的取值分别是:0分,1000分,3000分
(2)由已知得,转动A盘得到积分的概率为
转动B盘得到积分的概率为
设先转A盘所得的积分为X分,先转B盘所得的积分为Y分,则有
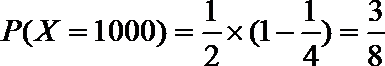
同理:
故先转A盘时,赢得积分平均水平较高。
解析
解析已在路上飞奔,马上就到!
知识点
17. 某射击游戏规定:每位选手最多射击3次;射击过程中若击中目标,方可进行下一次射击,否则停止射击;同时规定第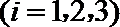


(Ⅰ)求甲恰好射击两次的概率;
(Ⅱ)设该选手甲停止射击时的得分总和为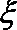
正确答案
(Ⅰ)设选手甲第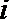
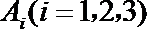
则
依题可知: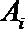
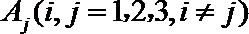
所求为:
(Ⅱ)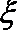
分布列为:
解析
解析已在路上飞奔,马上就到!
知识点
11.已知P是



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.某人居住在城镇的A处,准备开车到单位B处上班. 若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为

(1)请你为其选择一条由A到B的最短路线(即此人只选择从西向东和从南向北的路线),使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车次数为随机变量

正确答案
(1)记路段MN发生堵车事件为MN.
因为各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,所以路线A→C→D→B中遇到堵车的概率P1为
1-P(
=1-[1-P(AC)][1-P(CD)][1-P(DB)]
=1-
同理:路线A→C→F→B中遇到堵车的概率P2为1-P(
路线A→E→F→B中遇到堵车的概率P3为1-P(
显然要使得由A到B的路线途中发生堵车事件的概率最小.只可能在以上三条路线中选择.
因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小。
(2)路线A→C→F→B中遇到堵车次数
答:路线A→C→F→B中遇到堵车次数的数学期望为
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析