- 随机事件及其概率
- 共504题
20. 某同学参加3门课程的考试。假设该同学第一门课程取得优秀成绩的概率为




(Ⅰ)求该生至少有1门课程取得优秀成绩的概率;
(Ⅱ)求

(Ⅲ)求数学期望
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 甲、乙两个篮球运动员互不影响地在同一位置投球,命中的概率分别为

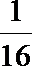
(1)求乙投球的命中率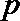
(2)若甲投球1次,乙投球2次,两人共命中的次数记为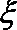
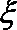
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.某地自行车的牌照号码由六个数字组成,号码中每个数字可以是



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.某班有50名学生,其中15人选修A课程,另外15人选修B课程,其它人不选任何课程,从中任选两名学生,则他们选修不同课程的学生概率为______。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.袋中装有35个球,每个球上都标有1到35的一个号码,设号码为n的球重
(1)如果任取1球,试求其重量大于号码数的概率;
(2)如果不放回任意取出2球,试求它们重量相等的概率;
(3)如果取出一球,当它的重量大于号码数,则放回,搅拌均匀后重取;当它的重量小于号码数时,则停止取球.按照以上规则,最多取球3次,设停止之前取球次数为

正确答案
解:(1)由
可得

由于
故
(2)因为是不放回任意取出2球,故这是编号不相同的两个球,设它们的编号分别为
由


故概率为
(3)




∴E

解析
解析已在路上飞奔,马上就到!
知识点
14.天气预报说,在今后的三天中每一天下雨的概率均为40%,用随机模拟的方法进行试验,由1、2、3、4表示下雨,由5、6、7、8、9、0表示不下雨,利用计算器中的随机函数产生0〜9之间随机整数的20组如下:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
通过以上随机模拟的数据可知三天中恰有两天下雨的概率近似为_________
正确答案
0.25
解析
解析已在路上飞奔,马上就到!
知识点
4.袋中有6个小球,分别标有数字1,2,3,4,5,6,甲乙两人玩游戏,先由甲从袋中任意摸出一个小球,记下号码


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 某校高二年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查.根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组
①[0,30),②[30,60),③[60,90),④[90,120),
⑤[120,150),⑥[150,180),⑦[180,210),⑧[210,240),
得到频率分布直方图如下.已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人;
(1)求n的值并补全下列频率分布直方图;
(2)如果把“学生晚上有效时间达到两小时”作为是否充分利用时间的标准,对抽取的n名学生,完成下列2×2列联表:
是否有95%的把握认为学生利用时间是否充分与走读、住宿有关?
参考公式:
参考列表:
(3)若在第①组、第②组、第⑦组、第⑧组中共抽出3人调查影响有效利用时间的原因,记抽到“有效学习时间少于60分钟”的学生人数为X,求X的分布列及期望;
正确答案
(1)设第i组的频率为Pi(i=1,2,…,8),
则由图可知:P1=×30=,P2=×30=
∴学习时间少于60钟的频率为:P1+P2= 由题n×=5 ∴n=100
又P3=×30=, P5=×30=, P6=×30=, P7=×30=, P8=×30=,
∴P4=1-(P1+P2+P3+P5+P6+P7+P8)=1-=1-=
第④组的高度h=×==
频率分布直方图如图:(未标明高度1/120扣1分)
(2)
K2=≈5.556
由于K2>3.841,所以有95%的把握认为
学生利用时间是否充分与走读、住宿
有关
(3)由(1)知:第①组1人,
第②组4人,第⑦组15人,第⑧组10人,总计20人。则X的所有可能取值为0,1,2,3
P(X=i)=(i=0,1,2,3)
∴P(X=0)= ==, P(X=1)= ===, P(X=2)= ===, P(X=3)= ===
∴X的分布列为:
EX=0×+1×+2×+3×===
(或由X服从20,5,3的超几何分布,∴EX=3×=)
解析
解析已在路上飞奔,马上就到!
知识点
8.中国女排战胜日本队的概率为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.甲、乙两名同学在5次英语口语测试中的成绩统计如下面的茎叶图所示.
(Ⅰ)现要从中选派一人参加英语口语竞赛,从统计学角度,你认为派哪位学生参加更合适,请说明理由;
(Ⅱ)若将频率视为概率,对学生甲在今后的三次数学竞赛成绩进行预测,记这三次成绩中高于80分的次数为


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析


























