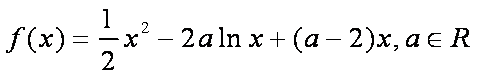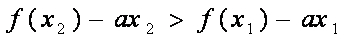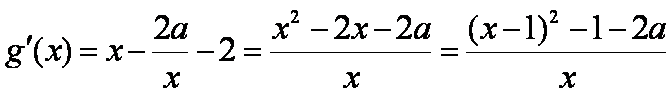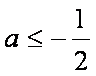- 圆系方程
- 共77题
1
题型:
单选题
|
已知半径为5的球O被互相垂直的两个平面所截,得到的两个圆的公共弦为4,若其中的一圆的半径为4,则另一圆的半径为
正确答案
D
解析
略
知识点
圆系方程
1
题型:简答题
|
已知⊙O1和⊙O2的极坐标方程分别是

若两圆的圆心距为,求a的值。
正确答案
见解析
解析
由ρ=2cosθ,
所以⊙O1的直角坐标方程为x2+y2=2x。
即 (x-1)2+y2=1。
由 ρ=2asinθ,得ρ2=2aρsinθ。
所以⊙O2的直角坐标方程为x2+y2=2ay,
即 x2+(y-a)2=a2。
⊙O1与⊙O2的圆心之间的距离为=,解得a=±2。
知识点
圆系方程
1
题型:
单选题
|
已知函数


正确答案
B
解析
略
知识点
圆系方程
1
题型:简答题
|
已知x、y、z均为正数,求证
正确答案
见解析
解析
因为x、y、z都是正数,所以
同理可得
将上述三个不等式两边分别相加,并除以2,得
知识点
圆系方程
1
题型:简答题
|
已知函数
(1)当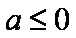
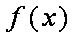
(2)是否存在实数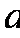


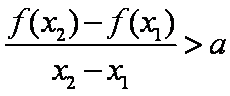
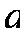
正确答案
见解析
解析
解析:
(1)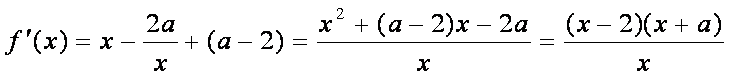
①当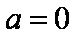
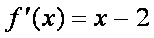
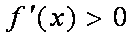
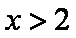
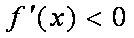
②当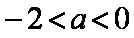
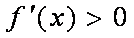
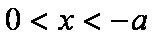
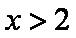
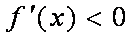

③当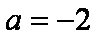
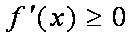
④当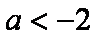
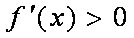
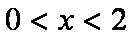
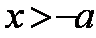
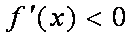
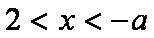
综上,当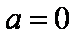
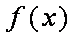
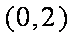
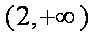
当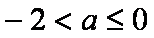
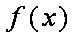

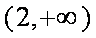
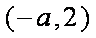
当
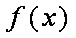
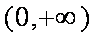
当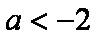
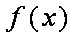
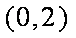

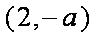
(2)∵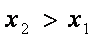
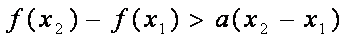
令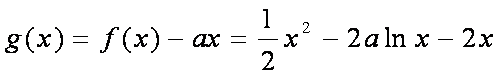
要使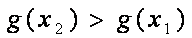
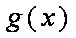
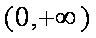
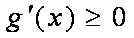
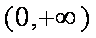
因此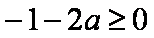
故存在实数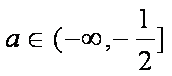

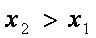
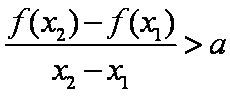
知识点
圆系方程
下一知识点 : 相交弦所在直线的方程
扫码查看完整答案与解析