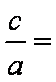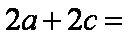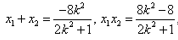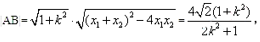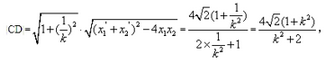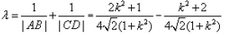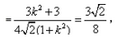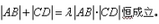- 函数单调性的性质
- 共479题
已知函数
(1)求函数
(2)若




正确答案
见解析。
解析
(1)令

由此可得所求函数的定义域为
(2)当


取等条件是


原不等式等价于

又
当




知识点
在平面直角坐标系








(1)求直线
(2)试判断直线




正确答案
见解析
解析
解析:
(1)由直线


所以直线
当




所以直线
(2)直线





又点P到直线



设直线






知识点
设


(1)若

(2)设过定点





(3)设


正确答案
见解析
解析
解法一:易知
所以

故-2
(2)显然直线

联立

∴
由

又0°<∠MON<90°

又
∵

故由①、②得
(3)解法一:根据点到直线的距离公式和①式知,点






当



解法二:由题设,

设



故四边形

当


知识点
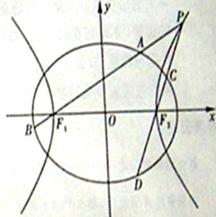
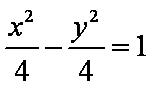
如图,已知椭圆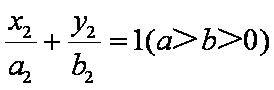
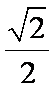
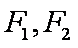
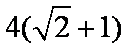
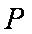
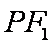
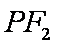
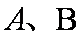
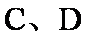
(1)求椭圆和双曲线的标准方程;
(2)设直线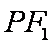
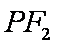
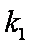
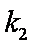
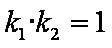
(3)是否存在常数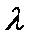
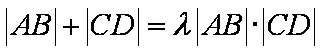
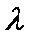
正确答案
见解析。
解析
(1)由题意知,椭圆离心率为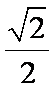
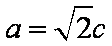
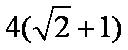
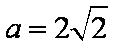
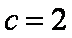
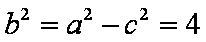

(2)设点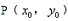
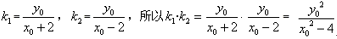
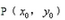
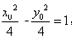
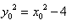
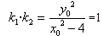
(3)假设存在常数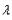
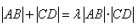
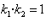
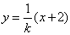
由方程组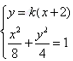
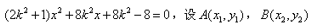
则由韦达定理得
所以
同理可得
又因为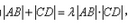
所以存在常数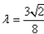
知识点
设|a|<1,函数f(x)=ax2+x-a(-1≤x≤1),证明:|f(x)|≤
正确答案
见解析
解析
证:|f(x)|=|a(x2-1)+x|≤|a(x2-1)|+|x|≤|x2-1|+|x|=1-x2+|x|=-(|x|-

∴|f(x)|≤
知识点
扫码查看完整答案与解析