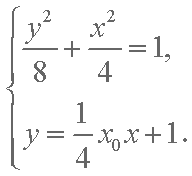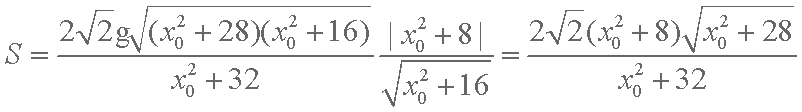- 函数单调性的性质
- 共479题
如图,已知点O是边长为1的等边

正确答案
解析
设E,F分别是AC,AB的中点,则BE=CF=




知识点
已知椭圆C: 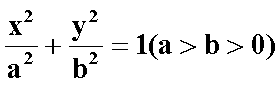
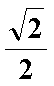
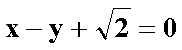
(1)求椭圆C的方程;
(2)若过点M(2,0)的直线与椭圆C交于两点A和B,设P为椭圆上一点,且满足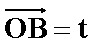
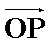
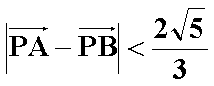
正确答案
(1)
(2)
解析
(1) 由题意知,短半轴长为: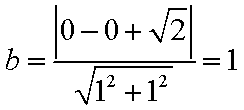
∵
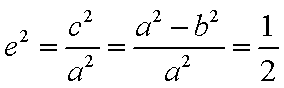
即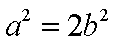
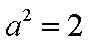
故椭圆

(2)由题意知,直线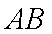


设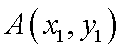

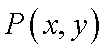
由




∵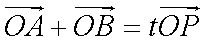
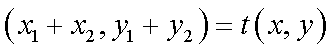
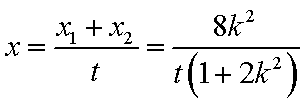

∵点

∴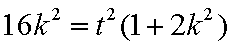
∵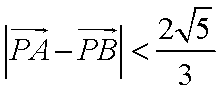
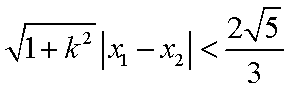
∴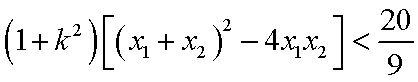
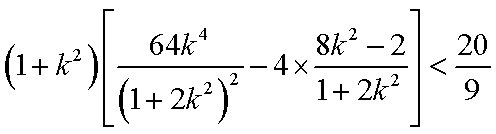
∴

∴
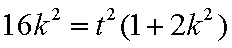
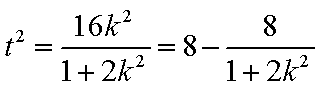
∴

∴实数
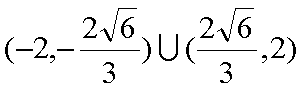
知识点
已知函数
(1)若函数
(2)若函数





正确答案
见解析。
解析
(1) 函数
因为



1)当



2)当

则有
因为



若函数

因为
综上,函数


(2)因为函数
即
所以
令
所以
当


所以
所以


所以

当

所以函数


又因为

所以


所以
综上,对任意的正整数n,当

知识点
如图1,在△ABC中,BC=3,AC=6,∠C=90°,且DE∥BC,将△ADE沿DE折起到△A1DE的位置,使A1D⊥CD,如图2。
(1)求证:BC⊥平面A1DC;
(2)若CD = 2,求BE与平面A1BC所成角的正弦值。
正确答案
见解析。
解析
以D为原点,分别以
建立空间直角坐标系D-xyz …………5分
说明:建系方法不唯一 ,不管左手系、右手系只要合理即可
在直角梯形CDEB中,过E作EF



设平面A1BC的法向量为




设BE与平面A1BC所成角为

知识点
已知椭圆


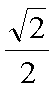
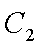
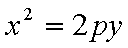
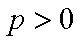


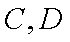
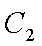


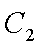

(1)求
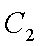
(2)求
正确答案
见解析
解析
(1)∵
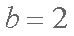
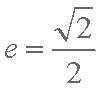

∴
∵
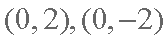
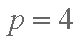
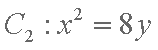
(2)设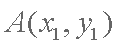
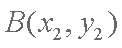

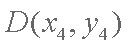

由(1)知
∴过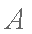

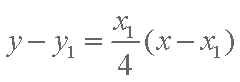

过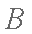

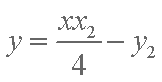
又∵这两条直线均过点
∴

∴点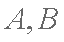
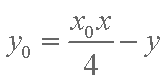
∴直线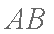
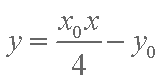
又∵直线AB过点

∴直线AB的方程为
解法一:联立方程组
得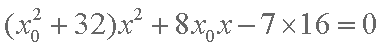


点


∴△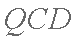
设
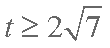
∴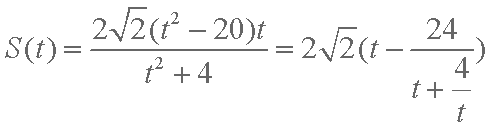
∴当

∴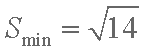
知识点
扫码查看完整答案与解析