函数单调性的性质_章节学习

1

题型：单选题

|

单选题 · 5 分

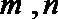
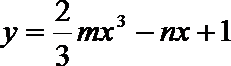
7．将一颗骰子抛掷两次，所得向上点数分别为，则函数在上为增函数的概率是（）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质古典概型的概率

1

题型：填空题

|

填空题 · 4 分

9．在极坐标系中，直线与直线的夹角大小为（）．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

1

题型：简答题

|

简答题 · 14 分

20．已知函数

（Ⅰ）当时，求函数的极小值；

（Ⅱ）当时，过坐标原点作曲线的切线，设切点为，求实数的值；

（Ⅲ）设定义在上的函数在点处的切线方程为

当时，若在内恒成立，则称为函数的“转

点”。当时，试问函数是否存在“转点”。若存在,请求出“转点”的横坐标,若不存在,请说明理由。

正确答案

（Ⅰ）当时，，

当时，；当时；当时.

所以当时，取到极小值。

（II)，所以切线的斜率

整理得,显然是这个方程的解，

又因为在上是增函数，

所以方程有唯一实数解，故.

(III)当时，函数在其图象上一点处的切线方程为

，

设，则，

若，在上单调递减，

所以当时，此时；

所以在上不存在“转点”.

若时,在上单调递减,所以当时, ，此时，

所以在上不存在“转点”.

若时，即在上是增函数，

当时，，

当时，，即点为“转点”，

故函数存在“转点”，且是“转点”的横坐标.

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

1

题型：简答题

|

简答题 · 18 分

23．函数，，其中，若对任意，，则称在内为对等函数．

（1）指出函数，，在其定义域内哪些为对等函数；

（2）试研究对数函数（且）在其定义域内是否是对等函数？若是，请说明理由；若不是，试给出其定义域的一个非空子集，使在所给集合内成为对等函数；

（3）若，且在内为对等函数，对于下列三组问题只需选做一种，满分分别是①3分，②6分，③8分；若选择了多于一种的情形，则按照序号较小的解答计分。

①举一例说明满足条件的函数可以既不是奇函数也不是偶函数；

②若对任意，都有，求证：为偶函数；

③试研究：在不同条件下，函数的奇偶性。

正确答案

（1），是对等函数；

（2）研究对数函数，其定义域为，所以，又，所以当且仅当时成立．所以对数函数在其定义域内不是对等函数．（分类讨论举也可）····

当时，若，则，此时是对等函数；

总之，当时，在及其任意非空子集内是对等函数；

当时，在及其任意非空子集内是对等函数．

（3）①例如函数；（为正数即可，例子不唯一）

②若对任意都有．当时，，

当时，，则有；

综上讨论，当时，若，则是偶函数．

③1）若对任意，都有．则是偶函数．证明见②

2）若对任意，都有当时，，当时，，则有；又综上讨论，若当时，，则是奇函数．

3）若存在，使得，也存在，使得，例如①，则既不是奇函数也不是偶函数。

4）若函数，则既是奇函数也是偶函数。

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

1

题型：单选题

|

单选题 · 5 分

9．已知等差数列中，，记数列的前项和为，若，对任意的成立，则整数的最小值为（）

A5

B4

C3

D2

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

1

题型：单选题

|

单选题 · 5 分

2．已知，，则“”是“”的（）

A充分不必要条件

B必要不充分条件

C充要条件

D既不充分也不必要条件

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

1

题型：简答题

|

简答题 · 14 分

20．已知椭圆的中心在坐标原点，焦点在轴上，短轴长为2，且两个焦点和短轴的两个端点恰为一个正方形的顶点。过右焦点与轴不垂直的直线交椭圆于，两点。

（Ⅰ）求椭圆的方程；

（Ⅱ）当直线的斜率为1时，求的面积；

（Ⅲ）在线段上是否存在点,使得以为邻边的平行四边形是菱形？

若存在，求出的取值范围；若不存在，请说明理由。

正确答案

（Ⅰ）由已知，椭圆方程可设为．

∵ 两个焦点和短轴的两个端点恰为正方形的顶点，且短轴长为2，

∴ ．

所求椭圆方程为．

（Ⅱ）右焦点，直线的方程为．

设，

由得，解得．

∴ ．

（Ⅲ）假设在线段上存在点,使得以为邻边的平行四边形是菱形．因为直线与轴不垂直，所以设直线的方程为．

由可得．

∴．

．其中

以为邻边的平行四边形是菱形

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

1

题型：简答题

|

简答题 · 12 分

16．设函数．

（Ⅰ）求函数的最小正周期和单调减区间；

（Ⅱ）将函数的图象向右平移个单位长度后得到函数的图象，求函数在区间上的最小值．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

1

题型：单选题

|

单选题 · 5 分

8．某程序框图如图所示，若使输出的结果不大于 37，则输入的整数i的最大值为（）

A3

B4

C5

D6

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

1

题型：单选题

|

单选题 · 5 分

10．已知为线段上一点，为直线外一点，为上一点，满足，，，且，则的值为（）

A

B3

C4

D5

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点