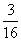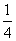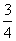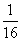- 函数单调性的性质
- 共479题
如图,在几何体
(1)求SC与平面SAB所成角的正弦值;
(2)求平面SAD与平面SAB所成的锐二面角的余弦值
正确答案
见解析。
解析
如图,过D作DC的垂线交SC于点E,
以点D为原点,分别以DC,DE,DA为

得
轴的距离为1,到

则
(1)设平面SAB的法向量为






而
(2)设平面SAD的法向量 为



从而

知识点
若实数



正确答案
解析
略
知识点
已知函数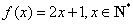
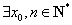
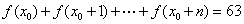
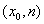
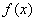
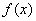
正确答案
解析
略
知识点
某游戏规则如下:随机地往半径为1的圆内投掷飞标,若飞标到圆心的距离大于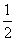
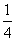
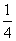
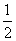
正确答案
解析
略
知识点
已知函数



(1)当

(2) 若



正确答案
(1) 


(2)
解析
(1)因为

因为函数


当




………………5分
所以

单调递减区间为
(2)因为
令

因为

当



所以




当
当




所以最大值1可能在

而
所以

当




所以最大值1可能在

而
所以
解得

当



所以最大值1可能在

综上所述,

知识点
扫码查看完整答案与解析