函数单调性的性质
共479题

· 函数单调性的性质

函数单调性的性质
共479题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

11．设是双曲线的两个焦点, 是上一点,若且的最小内角为,则的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：单选题

单选题 · 5 分

1．若z是复数，且（为虚数单位），则z的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：简答题

简答题 · 12 分

16．在△ABC中，分别为角的对边，已知向量与向量的夹角为，

求：（ I ）角B 的大小；

（Ⅱ）的取值范围．

正确答案

解：（I）∵

, ∴

∵ ∴．

（II）由正弦定理得，

∵ ， ∴， ∴，

∴，故的取值范围是(1,

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：简答题

简答题 · 14 分

21．已知椭圆，椭圆以的长轴为短轴，且与有相同的离心率。

（1）求椭圆的方程；

（2）设O为坐标原点，点A，B分别在椭圆和上，，求直线的方程。

正确答案

（1）由已知可设椭圆的方程为

其离心率为，

故，

则

故椭圆的方程为

（2）解法一两点的坐标分别记为

由及（1）知，

三点共线且点，不在轴上，

因此可以设直线的方程为

将代入中，

得，

所以

将代入中，

则，

所以

由，

得，

即

解得，

故直线的方程为或

解法二两点的坐标分别记为

由及（1）知，

三点共线且点，不在轴上，

因此可以设直线的方程为

将代入中，

得，

所以

由，

得，

将代入中，

得，

即

解得，

故直线的方程为或．

（1）F抛物线C：x2=2py（p>0）的焦点F，

设M，，

由题意可知，

则点Q到抛物线C的准线的距离为

，

解得，

于是抛物线C的方程为．

（2）假设存在点M，使得直线MQ与抛物线C相切于点M，

而，，

，

由

可得，

，

则，

即，

而，

解得，点M的坐标为．

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：简答题

简答题 · 12 分

18．小白被“老大”找到了！小伙伴们喜大普奔啊有木有！为了答谢“老大”，小新他们决定帮助“老大”做一件事，就是调查双叶幼稚园小朋友在20：00～21：00时间段在做什么？最后小新等做成了下面的数据表：

（1）将此样本的频率作为总体的概率估计，随机调查3名男性小朋友，设调查的3名男性小朋友在这一时间段以看电视的人数为随机变量X，求X的分布列和期望；

（2）根据以上数据，吉永老师能否有99%的把握认为“在20：00～21：00时间段的休闲方式与性别有关系”？

参考公式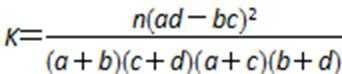：，其中n＝a＋b＋c＋d．

参考数据：

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

继续学习学习下一知识点

下一知识点 : 复合函数的单调性

百度题库 > 高考 > 理科数学 > 函数单调性的性质

扫码查看完整答案与解析