- 函数单调性的性质
- 共479题
12.已知函数f(x)是定义在R上的奇函数,并满足f(x-4)=-f(x)且在[0,2]上是增函数,给出下列结论:
(1)若0<x1<x2<4,且x1+x2=4,则f(x1)+f(x2)>0;
(2)若0<x1<x2<4,且x1+x2=5,则f(x1)>f(x2);
(3)若方程f(x)=m在[-8,8]内恰有四个不同的根x1,x2,x3,x4,则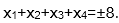
正确答案
解析
∵f(x-4)=-f(x),
∴f(x-8)=-f(x-4)=f(x),
∴f(x)的周期为8.
∵函数f(x)是定义在R上的奇函数,
∴f(x)关于原点对称.
∵f(x-4)=-f(x),∴f(x-4)=f(-x),
∴f(x)关于x=-2对称.
由f(x)关于原点对称,
∴f(x)也关于x=2对称.
由f(x)在[0,2]上是增函数,且f(0)=f(4)=0,则可以画出草图为
(1)若0<x1<x2<4,且x1+x2=4,则可得到x1,x2关于x=2对称,
由图可知f(x1)>0,f(x2)>0,
所以f(x1)+f(x2)>0,故(1)正确.
(2)若0<x1<x2<4,且x1+x2=5,则可得x2到x=2的距离比x1到x=2的距离要远,
由图象可得f(x1)>f(x2),故(2)正确.
(3)如图所示,若m>0,则两个根关于x=-6对称,两个根关于x=2对称,
所以有x1+x2+x3+x4=-8.若m<0,
则两个根关于x=-2对称,
两个根关于x=6对称,所以有x1+x2+x3+x4=8,
故(3)也正确.
本题答案为D.
知识点
12.已知函数f(x)是定义在R上的奇函数,并满足f(x-4)=-f(x)且在[0,2]上是增函数,给出下列结论:
(1)若0<x1<x2<4,且x1+x2=4,则f(x1)+f(x2)>0;
(2)若0<x1<x2<4,且x1+x2=5,则f(x1)>f(x2);
(3)若方程f(x)=m在[-8,8]内恰有四个不同的根x1,x2,x3,x4,则
正确答案
解析
∵f(x-4)=-f(x),
∴f(x-8)=-f(x-4)=f(x),
∴f(x)的周期为8.
∵函数f(x)是定义在R上的奇函数,
∴f(x)关于原点对称.
∵f(x-4)=-f(x),∴f(x-4)=f(-x),
∴f(x)关于x=-2对称.
由f(x)关于原点对称,
∴f(x)也关于x=2对称.
由f(x)在[0,2]上是增函数,且f(0)=f(4)=0,则可以画出草图为
(1)若0<x1<x2<4,且x1+x2=4,则可得到x1,x2关于x=2对称,
由图可知f(x1)>0,f(x2)>0,
所以f(x1)+f(x2)>0,故(1)正确.
(2)若0<x1<x2<4,且x1+x2=5,则可得x2到x=2的距离比x1到x=2的距离要远,
由图象可得f(x1)>f(x2),故(2)正确.
(3)如图所示,若m>0,则两个根关于x=-6对称,两个根关于x=2对称,
所以有x1+x2+x3+x4=-8.若m<0,
则两个根关于x=-2对称,
两个根关于x=6对称,所以有x1+x2+x3+x4=8,
故(3)也正确.
本题答案为D.
知识点
14.若

正确答案
-1
解析
∵ 
∴当
知识点
4.设直线x=t与函数f(x)=x2,g(x)=ln x的图象分别交于点M、N,·则当|MN|达到最小时t的值为( )
正确答案
解析
因为|MN|=f(x)-g(x)=x2-ln x.
令F(x)=x2-ln x,则F'(x)=2x-

所以当0<x<
当x>
故当x=
知识点
6.直线
正确答案
解析
∵ △AOB是直角三角形,
∴圆心(0,0)到直线的距离为
即
∴
故由二次函数性质知
知识点
扫码查看完整答案与解析








