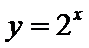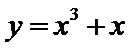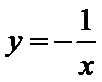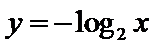函数单调性的性质
共479题

· 函数单调性的性质

函数单调性的性质
共479题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

12．已知函数,若对任意，，则（）

正确答案

解析

由题意得，函数在f(x)在x=1处取到最小值。

，所以，令求解方程，得到

，，所以当a>0时，函数得而单调递减区间是，单调递增区间是，于是可知，是函数的唯一极小值点，故，整理得，即

令，求导并令导函数为零，，得到，当

时，，函数单调递增，当时，，函数单调递减，因为，故，所以

即，所以选A。

考查方向

函数的单调性与导数的关系、函数的最值与导数的关系、不等式的定义与性质

解题思路

先判断函数的单调性，然后求导求最值。

易错点

函数单调性判断错误、求导错误

知识点

函数单调性的性质导数的运算其它不等式的解法

题型：单选题

单选题 · 5 分

3.下列函数在其定义域内既是奇函数又是增函数的是（）

正确答案

解析

根据函数的性质可以知道，A、B为增函数，B、C为奇函数，所以选B

考查方向

函数的奇偶性，函数的单调性

解题思路

先判定奇偶性再判定函数增减性

易错点

考虑函数奇偶性和单调性的时候，要注意函数的取值范围

知识点

函数单调性的性质

题型：单选题

单选题 · 5 分

10．函数是奇函数f（x）（x∈R）的导函数，f（1）=0，当x＜0时，，则使得f（x）＜0成立的x的取值范围是（　　）

A（﹣∞，﹣1）∪（0，1）

B（﹣1，0）∪（1，+∞）

C（﹣∞，﹣1）∪（1，+∞）

D（﹣1，0）∪（0，1）

正确答案

解析

考查方向

本题主要考查函数奇偶性，单调性及导函数运算和性质，不等式解法，数形结合思想的应用等知识,意在考查考生运算求解能力、分析问题和解决问题的能力，在近几年的各省高考题出现的频率较高，常与函数单调性、周期性、对称型、奇偶性等知识点交汇命题，较难。

解题思路

1、根据题意构造函数g（x）=xf（x）再得到函数g（x）的单调区间。

2、根据f（x）奇函数判断出g（x）是偶函数，将不等式进行转化，由图象求出不等式成立时x的取值范围即可。

易错点

1、本题由得不到函数模型，导致题目无法进行。

知识点

函数单调性的性质导数的运算其它不等式的解法

题型：简答题

简答题 · 12 分

21．已知函数．(Ⅰ)若直线与的反函数的图象相切，求实数k的值；(Ⅱ)设，且试比较三者的大小，并说明理由．

正确答案

(1)的反函数为设切点为则切线斜率为故

（2）不妨设令则所以在上单减，故取则令则在上单增，故取则综合上述知，

解析

反函数的应用很重要，学会灵活应用举一反三，导数的应用便于解决实际问题，利用导数求曲线的切线，导数与函数的单调性、最值，比较大小。

考查方向

利用导数求曲线的切线，导数与函数的单调性、最值，比较大小

解题思路

的反函数是，问题为求过原点所作曲线的切线的斜率，方法是设切点坐标为，由导数的几何意义可得解；（2）首先不妨设，要比较大小比较方便，只要作差，计算后因式分解可得

易错点

曲线“在点处的切线”与“过点的切线”的区别与联系

知识点

函数单调性的性质反函数导数的几何意义

题型：单选题

单选题 · 5 分

12．已知函数，其在区间上单调递增，则的取值范围为（）

正确答案

解析

令2x=t,(t>0)则当a=0时，y=t,符合题意；当a<0时，函数图像为“对勾函数”，只有a>=1才符合题意；同理，当a>0时，只有当a<=时符合题意。A选项不正确，B选项不正确，D选项不正确，所以选C选项。

考查方向

本题主要考查函数的性质的综合应用

解题思路

1、对a分类讨论；

2、代入不同的a值，画出函数图像，即可得到结果。

A选项不正确，B选项不正确，D选项不正确，所以选C选项。

易错点

本题易利用指数函数图像时发生错误。

知识点

函数单调性的性质指数函数的图像与性质

继续学习学习下一知识点

下一知识点 : 复合函数的单调性

百度题库 > 高考 > 理科数学 > 函数单调性的性质

扫码查看完整答案与解析